Исследование методов обеспечения заданной точности при сборке электронной аппаратуры, страница 2

            Основное преимущество данного метода перед методом полной взаимозаменяемости заключается в выборе более широких допусков на первичные параметры схемных элементов, принимая во внимание определенный процент риска. Для нормального закона распределения погрешностей выходных контролируемых параметров и заданного процента риска с помощью решения интеграла вероятностей Ляпунова можно рассчитать погрешности параметров с любой заданной степенью вероятности, которые учитываются с помощью коэффициента  относительного рассеивания выходного параметра   .

            Значения коэффициента относительного рассеивания  сведены в табл. 8.1 в зависимости от заданного процента риска.

                                                                                                                             Таблица 8.1.

Значения коэффициента относительного рассеяния

	Процент риска
	0,27	0,5	1,0	1,5	2,0	3,0	4,0	5,0	6,0	8,0	10,0
	1	1,05	1,11	1,17	1,21	1,26	1,30	1,33	1,36	1,40	1,44

            C учетом коэффициента относительного рассеивания рассчитанные поля рассеивания погрешностей выходных контролируемых параметров уменьшаются, а допуски на первичные параметры - увеличиваются

    .                                       (4)

            Метод групповой взаимозаменяемости. Сущность метода групповой взаимозаменяемости состоит в том, что требуемая точность выходных выходных контролируемых параметров узлов достигается включением в схему одного или нескольких схемных элементов с узкими допусками на их первичные параметры. С этой целью производится предварительная селекция или сортировка схемных элементов и последующее их комплектование, таким образом, чтобы осуществлялась взаимная компенсация их погрешностей.

            Дополнительные расходы, связанные с проведением селекции или сортировки элементов схемы должны окупаться за счет экономии, получаемой при изготовлении электрорадиоэлементов с более широкими допусками.

            Вместе с тем следует иметь в виду, что экономическая целесообразность использования метода групповой взаимозаменяемости значительно уменьшается при увеличении количества элементов, проходящих селекцию или сортировку и, за счет наличия незавершенного производства (т.е. остатков электрорадиоэлементов не вошедших в комплекты для сборки).

            Метод подгонки. Сущность метода состоит в том, что требуемая точность выходных контролируемых параметров изготавливаемых узлов достигается необратимым изменением параметра или подбором одного или нескольких схемных элементов с постоянными параметрами, применение которого в схеме узла обеспечивает частичную или полную компенсацию погрешностей выходных контролируемых параметров.

            Подгоняемый или подбираемый элемент называется компенсатором. В качестве компенсаторов рекомендуется выбирать элементы, с наибольшей чувствительностью, чтобы уменьшить объемы подгоночных операций или количество значений подбираемых параметров.

            Метод регулировки обеспечивает точность выходных контролируемых параметров изготавливаемых узлов путем обратимого изменения первичного регулируемого параметра компенсирующего элемента, в качестве которого применяют специальные схемные элементы с переменными параметрами - регулировочные элементы.

            Метод регулировки аналогичен методу подгонки. Однако в случае раскомпенсации имеется возможность ее восстановления. Регулировочный элемент с переменным параметром позволяет получить необходимую точность не только при изготовлении, но и в период эксплуатации. Он компенсирует производственные погрешности и погрешности, являющиеся следствием изменения температуры и старения схемных элементов.

            Наряду с достоинствами метод регулировки имеет недостатки: регулировочный элемент, поставленный в схему, снижает надежность аппаратуры, так как надежность регулировочных элементов значительно ниже надежности элементов с постоянными параметрами; кроме того наличие регулировочных элементов в схеме значительно усложняет технологический процесс изготовления аппаратуры, поскольку требует неоднозначного выбора набора регулировочных элементов, разработки стратегии регулировки и высокой квалификации регулировщиков.

2. Анализ методов сборки делителя напряжения

Схема делителя напряжения представлена на рис. 1. Основным выходным параметром делителя является коэффициент передачи (коэффициент деления) по напряжению

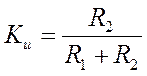.                                                         (5)

При этом .

Рис. 1. Электрическая схема делителя напряжения

Уравнение погрешности выходного контролируемого параметра  может быть записано следующим образом:

,

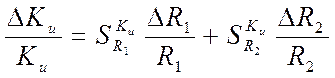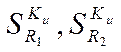где  - относительные погрешности сопротивлений резисторов , ; - чувствительности (коэффициенты влияния) выходного параметра  к вариациям первичных параметров сопротивлений резисторов , .

            Чувствительности 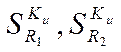, используя выражение (5), определяются следующим образом:

;

.

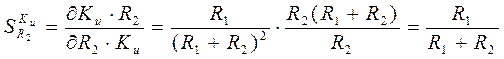            При , =и ; . Тогда уравнение погрешности запишется следующим образом

.

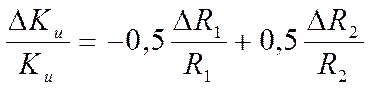            Сделаем следующие допущения.

1.  Закон распределения погрешностей схемных параметров – нормальный.

2.   Погрешности схемных параметров  и  не кореллированы

3.  Центр группирования совпадает с серединой поля допуска.

4.  В поле допуска находится 99,73% всех случайных отклонений.

5.  Выходной параметр , первичные параметры схемных элементов

Тогда можно записать, что , так как = .

Уравнение допусков при статистическом методе расчета с полной взаимозаменяемостью в данном случае запишется следующим образом:

полагая  =10% и ==, уравнение допусков перепишется в виде

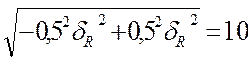 или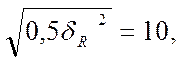тогда === =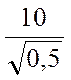14,3%.

            Расчет допусков по методу максимума-минимума в тех же условиях сводится к следующему

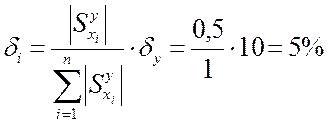, причем полная взаимозаменяемость будет выполняться независимо от вида законов распределения погрешностей.

            Из сравнения приведенных расчетов видим, что допуски рассчитанные по статистическому методу почти в три раза шире допусков, рассчитанных по методу максимума-минимума.