Система обеспечения теплового режима космического аппарата. Расчет характеристик систем обеспечения теплового режима космических аппаратов, страница 24

Для расчета высокотемпературных ТТ сравнительно часто используют линеаризованную модель Шиндлера и Веснера. В данной модели предполагается линейный характер изменения градиентов давления и температуры в жидкости и паре между зонами испарения и конденсации. Режимы течений жидкости и пара принимаются ламинарными и подчиняющимися закону Пуазейля. Из-за малости градиентов температуры и давления по длине тепловой трубы принимаются постоянными следующие величины:  Допустим, что тепловая труба работает в состоянии невесомости и не имеет транспортной зоны.

Тогда из уравнения (3.57) получим

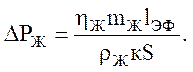
Примем  Окончательно получим:

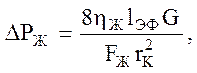                                                                                                 (3.58)

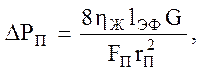                                                                                                    (3.59)

где G - объемный расход жидкости;

r - средний эффективный радиус поперечного сечения капилляра фитиля.

Для круглого канала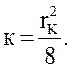  

Тогда

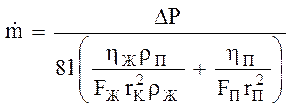
Из предпожения о том, что тепловой поток, участвующий в фазовых превращениях, без потерь передается ТТ, можем найти

где - скрытая теплота парообразования,

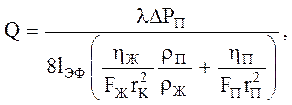                                            (3.60)

где 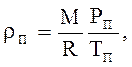   ,- температура и давление насыщенного пара.

Проницаемость  в выражении (3.57) учитывает размер пор, их извилистость и распределение и представляет собой эффективную площадь поперечного сечения в пористом теле для прохождения жидкости.

Для капиллярных структур из шариков

где - диаметр шарика;  - пористость фитиля.

Для сетчатых фитилей

где - диаметр проволоки.

Для металло-войлока и тканевого материала

где - эффективный диаметр поры.

Для сеточных фитилей величина  обычно заключается в пределах (2…6)10^{-10 м2}.

Пористость  характеризуется отношением объема пустот к объему фитиля [17]:

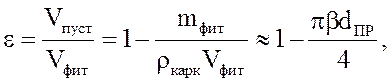
где ,  - масса и объем фитиля;    - плотность материала каркаса фитиля;   - фактор, характеризующий изгибы проволоки            N - число ячеек на единицу длины.

Для идеального газа перепад давления  и температурный перепад  при заданной рабочей температуре ТТ связаны соотношением Клайперона-Клаузиуса

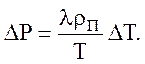                                                              (3.61)

Тогда

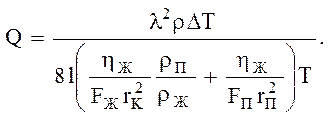                                  (3.62)

Соотношения (3.60) и (3.62) позволяют рассчитывать рабочие характеристики ТТ  и  при заданных геометрических размерах ТТ и капиллярной структуры.

Расчет выполняется в следующем порядке:

1) задается средняя рабочая температура тепловой трубы Т, по которой выбираются теплофизические параметры жидкого и парообразного теплоносителя;

2) при заданной температуре Т (Т = const) определяется Q в зависимости от температурного перепада

3) задаваясь целым рядом рабочих температур ТТ и определяя зависимость ее теплопередающей способности от  для каждого значения заданной температуры, получают рабочие характеристики .

В работе [18] подробно изложена методика расчета регулируемых ТТ для упрощенного случая, когда неконденсирующийся газ подчиняется уравнению состояния идеального газа.

Расчет тепловых труб с помощью номограмм Андела

С целью облегчения расчета ТТ для известных жидкометаллических теплоносителей Е.Анделом [19] построены номограммы. На рис.3.8 приведена номограмма для определения предельного значения теплового потока, передаваемого ТТ с оптимизированной капиллярной структурой в виде продольных борозд. Номограмма состоит из шести вертикалей, на которых нанесены характерные параметры ТТ, а справа от вертикалей располагаются точки, соответствующие различным теплоносителям. На вертикали I отложено отношение эффективной длины ТТ к диаметру парового канала  на вертикали II – диаметр парового канала, см.; на вертикалях IV и VI отложены максимальная теплопередающая способность ТТ  и температура в зоне испарения .

При известной геометрии ТТ расчет с помощью номограммы следует проводить в следующем порядке. Определяется отношение  и отсчитывается на I вертикали. Через полученную точку и точку, соответствующую данному диаметру ТТ, проводят линию до пересечения с вертикалью III. Справа на номограмме проводят другую линию через точку, соответствующую заданному теплоносителю, и точку на вертикали VI, соответствующую заданной температуре, до пересечения с вертикалью V.