Электрические цепи постоянного тока и методы их расчета. Режимы работы электрической цепи. Основные методы расчета сложных электрических цепей, страница 4

(1.7)

.

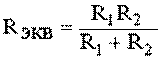Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:

g_экв = g₁ + g₂ + g₃.

По мере роста числа параллельно включенных потребителей проводимость цепи gэкв возрастает, и наоборот, общее сопротивление R_экв уменьшается.

Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)

U = IR_экв = I₁R₁ = I₂R₂ = I₃R₃.

Отсюда следует, что

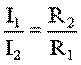, т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.

По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.

Электрическая цепь со смешанным соединением элементов

Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.

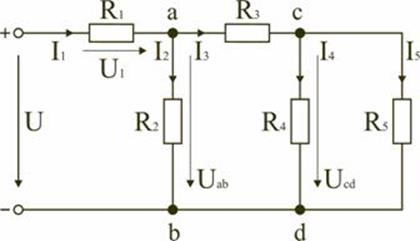
Рис. 1.7

Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R₁=R₂=R₃=R₄=R₅=R. Сопротивления R₄ и R₅ включены параллельно, тогда сопротивление участка цепи cd равно:

.

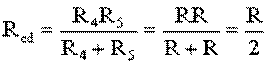В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):

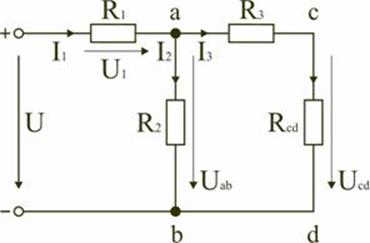
Рис. 1.8

На схеме (рис. 1.8) сопротивление R₃ и R_cd соединены последовательно, и тогда сопротивление участка цепи ad равно:

.

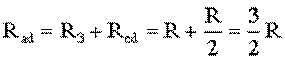Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):

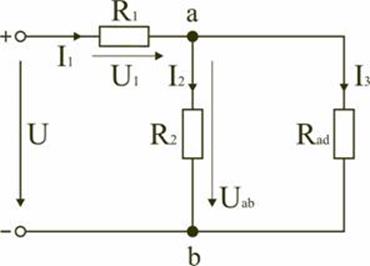
Рис. 1.9

На схеме (рис. 1.9) сопротивление R₂ и R_ad соединены параллельно, тогда сопротивление участка цепи аb равно

.

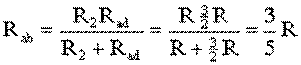Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R₁ и R_ab включены последовательно.

Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:

.

Рис. 1.10

Рис. 1.11

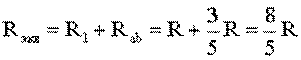В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R_экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.

Соединение элементов электрической цепи по схемам «звезда» и «треугольник»

В электротехнических и электронных устройствах элементы цепи соединяются по мостовой схеме (рис. 1.12). Сопротивления R₁₂, R₁₃, R₂₄, R₃₄ включены в плечи моста, в диагональ 1–4 включен источник питания с ЭДС Е, другая диагональ 3–4 называется измерительной диагональю моста.

Рис. 1.12

Рис. 1.13

В мостовой схеме сопротивления R₁₃, R₁₂, R₂₃ и R₂₄, R₃₄, R₂₃ соединены по схеме «треугольник». Эквивалентное сопротивление этой схемы можно определить только после замены одного из треугольников, например треугольника R₂₄ R₃₄ R₂₃ звездой R₂ R₃ R₄ (рис. 1.13). Такая замена будет эквивалентной, если она не вызовет изменения токов всех остальных элементов цепи. Для этого величины сопротивлений звезды должны рассчитываться по следующим соотношениям:

(1.8)

; ; .

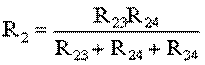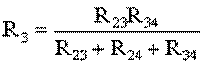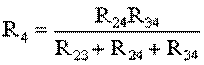Для замены схемы «звезда» эквивалентным треугольником необходимо рассчитать сопротивления треугольника:

(1.9)

; ; .

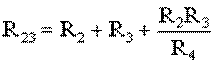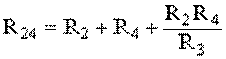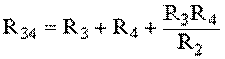После проведенных преобразований (рис. 1.13) можно определить величину эквивалентного сопротивления мостовой схемы (рис. 1.12)

.

1.5. Источник ЭДС и источник тока в электрических цепях

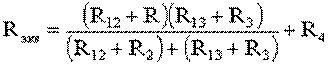При расчете и анализе электрических цепей реальный источник электрической энергии с конечным значением величины внутреннего сопротивления r₀ заменяют расчетным эквивалентным источником ЭДС или источником тока.

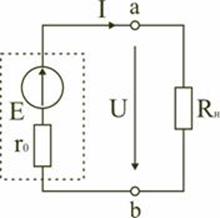Рис. 1.14

Источник ЭДС (рис. 1.14) имеет внутреннее сопротивление r₀, равное внутреннему сопротивлению реального источника. Стрелка в кружке указывает направление возрастания потенциала внутри источника ЭДС.