Балтийский Государственный Технический Университет им. Д.Ф.Устинова
«ВОЕНМЕХ»
Кафедра электротехники.
Курсовая работа по электротехнике.
Тема:
ПЕРЕХОДНЫЕ ПРОЦЕССЫ В
ЭЛЕКТРИЧЕСКИХ ЦЕПЯХ.
Вариант №1
Студент Бородин А. Ю.
Группа: Е-651
Преподаватель: Погромская Л.Ф.
Оценка:
Подпись:
Санкт-Петербург
2007г.
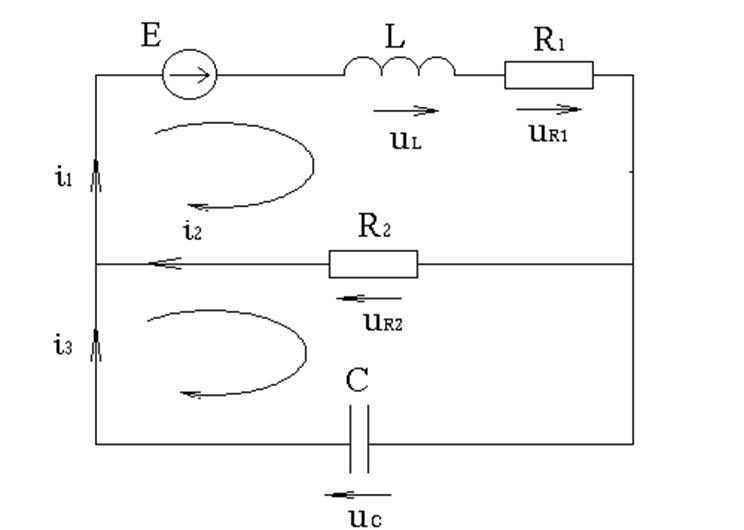
1. Схема.
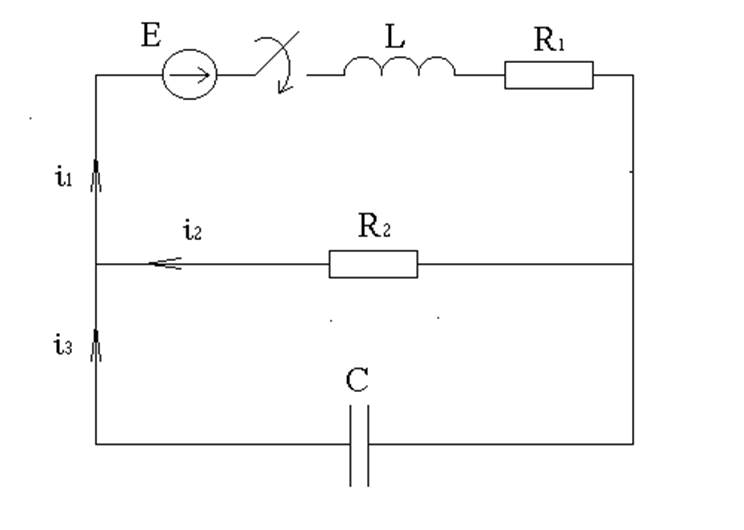 |
ПАРАМЕТРЫ ЦЕПИ:
E = 110 В
L = 0.5 Гн
R1 = 600 Ом
R2 = 1000 Ом
С = 10 мкФ
2. Составление характеристического уравнения по Zвх и расчет его корней.
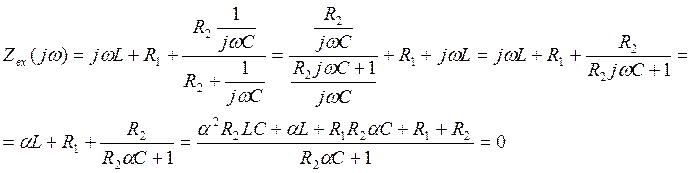 (2.1)
(2.1)
![]() (2.2)
(2.2)
![]() | :
R2LC (2.3)
| :
R2LC (2.3)

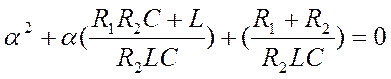 (2.4)
(2.4)
где ![]()
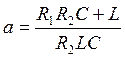 и
и 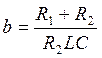
рассчитаем a и b:
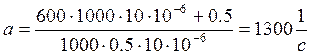 (2.5)
(2.5)
(2)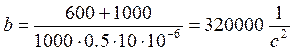
(2.6)
![]() , откуда
, откуда
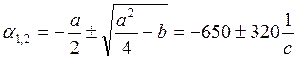 (2.7)
(2.7)
Корни:
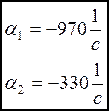 (2.8)
(2.8)
|
|
|
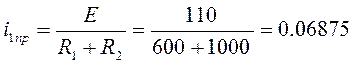 A (3.1)
A (3.1)
![]() А
(3.2)
А
(3.2)
![]() А
(3.3)
А
(3.3)
![]() В (3.4)
В (3.4)
![]() В (3.5)
В (3.5)
![]() B (3.6)
B (3.6)
![]() B (3.7)
B (3.7)
4. Определение начальных условий:
а) Независимые начальные условия.(ННУ)
![]() (4.1)
(4.1)
![]() (4.2)
(4.2)
б) Зависимые начальные условия.(ЗНУ)
|
|
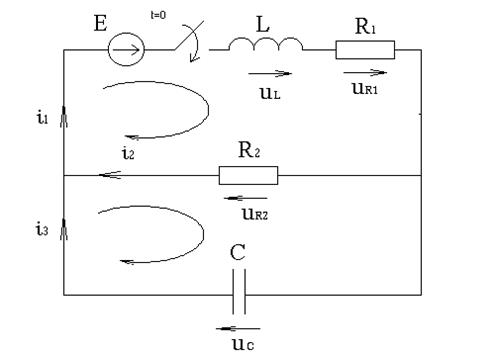
Составим систему уравнений по з.К:
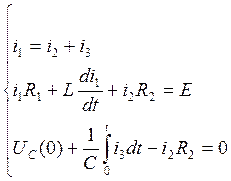 (4.3)
(4.3)
Подставим независимые начальные условия в систему уравнений и положим время t=0:
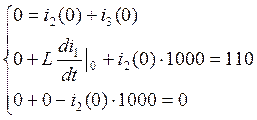 (4.4)
(4.4)
![]() (4.5)
(4.5)
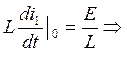
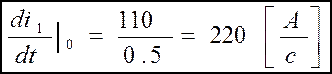 (4.6)
(4.6)
![]() (4.7)
(4.7)
5.
Составление ДУ по законам Кирхгофа: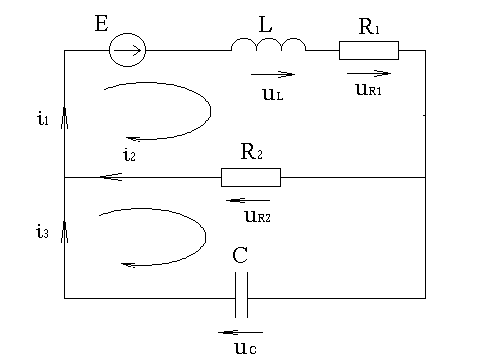

Выразим из (5.1) ![]() :
:
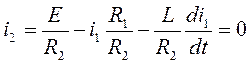 (5.4)
(5.4)
Подставим в (5.3) и продифференцируем выражение:
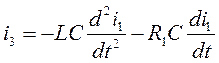 (5.5)
(5.5)
Подставим (5.4) и (5.5) в(5.1)
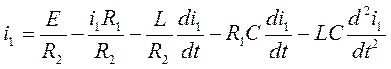 (5.6)
(5.6)
Откуда, разделив обе части уравнения на LC и выполнив образования, получаем:
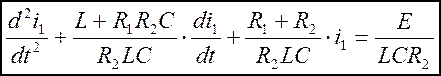 (5.7)
(5.7)
Получили дифференциальное уравнение 2-го порядка (т.к в схеме 2 независимых реактивных элемента).
6. Составление ДУ методом Д-алгебраизации:
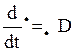
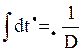

Приведём систему уравнений к следующему виду:

Из (6.3): i3=i1-i2 (6.7)
Подставим (6.4) в (6.5),(6.6):
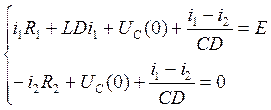 (6.8)
(6.8)
Получим:
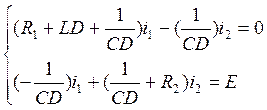 (6.9)
(6.9)
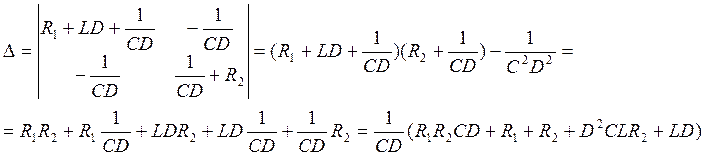 (6.10)
(6.10)
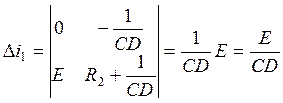 (6.11)
(6.11)
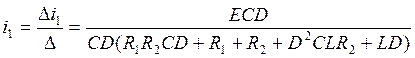 (6.12)
(6.12)
![]() |
: LCR2 (6.13)
|
: LCR2 (6.13)
Произведя обратные преобразования получим:
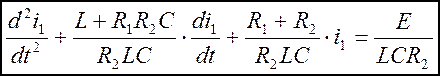 (6.14)
(6.14)
7. Анализ полученного дифференциального уравнения:
а) Проверка размерности a и b:
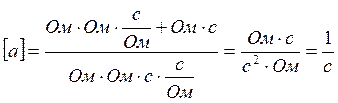 (7.1)
(7.1)
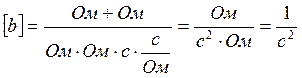 (7.2)
(7.2)

б) Проверка правой части:
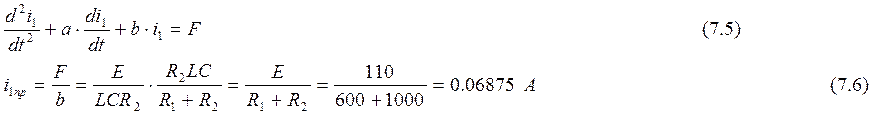
8. Решение полученного ДУ классическим методом относительно iL:
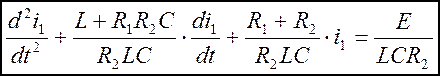 (8.1)
(8.1)
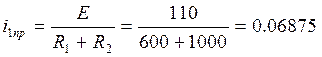 A (8.2)
A (8.2)
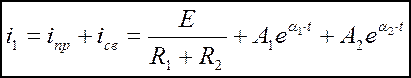 (8.3)
(8.3)
при t=0:
![]() , (8.4)
, (8.4)
где из (16)
![]() (8.5)
(8.5)
из (8.4),(8.5):
А2= -0.06875-А1 (8.6)
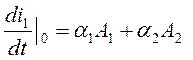 (8.7)
(8.7)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.