Осколочная боевая часть стержневого типа со скрепленными концами стержней, страница 2

В период пассивной фазы происходит полет стержней по инерции. При рассмотрении этой фазы примем допущение что импульс заряда ВВ выровнен вдоль стержневой оболочки и все сечения стержня движутся с одинаковой начальной скоростью. Ввиду того что длительность активной фазы намного меньше (в 10⁹ раз) длительности пассивной фазы, при рассмотрении   движения стержневого кольца будем считать, что движение начинается с поверхности заряда ВВ с некоторой начальной скоростью   (- вектор, который в каждом сечении стержня совпадает с направлением радиуса разрывного заряда, проведенного через это сечение

Рисунок 1

упрощенная схема движения пары стержней стержневой оболочки -рисунок 1

Рассмотрим движение пары стержней длиной , и шириной , уложенных на поверхности цилиндрического заряда под некоторым углом  к его образующей (влиянием торцевого разлета стержня пренебрегаем).

На практике угол  смещения концов стержней в плоскости перпендикулярной образующей заряда ВВ, мал( ), поэтому можно считать, что оба стержня лежат в плоскости X.

Тогда

Поскольку расстояние между центрами концов стержней: 

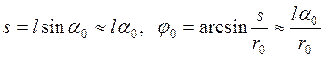
то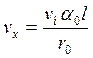

Так как соединенные стержни, уложенные на поверхности заряда, ассиметричны относительно плоскости, проходящей через их центры масс, но симметричны относительно противоположных пар, то достаточно рассмотреть пару полустержней длиной   (- эффективная длина стержня, т.е. длина стержня без участка соединения их).

Рисунок 2

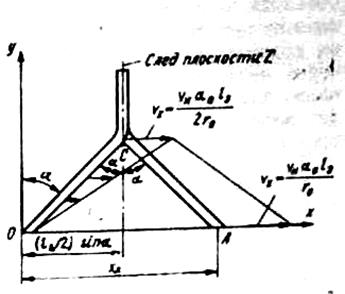
Движение пары стержней, так же как и отдельного стержня, является сложным, состоящим из переносного движения общего центра масс и относительного движения стержней около этого центра .

Переносное движение, есть поступательное движение со скоростью  вдоль прямой, являющийся продолжением радиуса заряда, проходящего через общий центр масс пары.

Для оценки влияния совместного движения пары стержней на отдельно взятый стержень необходимо рассмотреть пару в ее относительном движении. (рис) Относительное движение стержней вызвано наличием составляющей , имеющей в плоскости сечения, проходящей через центр массы стержня , величину 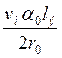 и направленной влево для левого полустержня и вправо, когда движение пары будет определятся скоростями на рис 7.

В процессе раскрытия стержневого кольца вблизи места соединения стержней образуется пластический шарнир, поэтому движение пары можно рассматривать как движение шарнирно закрепленных в точке С элементов, закрепленных в точке О, при наличии вектора скорости, приложенного в точке А и направленного по прямой ОА.

Из рис. видно , продифференцировав это выражение по времени и вынося производные получим:

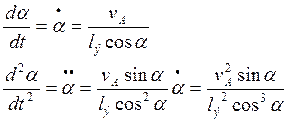
Учитывая, что

R – текущий радиус раскрытия стержневого кольца;  - теоретический радиус раскрытия стержневого кольца;- относительный радиус; N – количество стержней.

Получим следующие уравнения для угловой скорости  и углового ускорения  стержня.

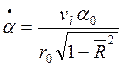
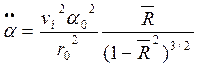
Обозначив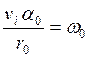

           ;

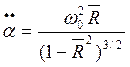Таким образом, относительным движением стержней является вращение их относительно собственного центра масс с угловым ускорением . При   . Тогда 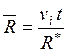 и зависимости  можно представить как функции времени разлета стержней:

         (*)

      (**)

4.Расчет усилий в стержнях и их соединениях.

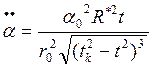Уравнение, описывающее относительное движение стержня, выведем с учетом взаимного влияния стержней в результате их соединения. На пару полустержней со стороны

«отброшенной» части стержневого кольца будет оказываться воздействие, которое можно представить силой, составляющая которой  , приложенная к точке А, вызывает относительное движение пары полустержней.

Рисунок 3