Проверка статистических гипотез о числовых значениях нормальных распределений в математических пакетах STATGRAPHICS и MATHCAD

Галушкин И. В. Е-441

Прикладная статистика.

Лабораторная работа № 5.

Проверка статистических гипотез о числовых значениях нормальных распределений в математических пакетах STATGRAPHICS и MATHCAD.

Вариант № 2:

STATGRAPHICS:

One-Variable Analysis - NORMAL

Analysis Summary

Data variable: NORMAL

50 values ranging from 1,49722 to 5,8264

The StatAdvisor

--------------This procedure is designed to summarize a single sample of data.

It will calculate various statistics and graphs.  Also included in the

procedure are confidence intervals and hypothesis tests.  Use the

Tabular Options and Graphical Options buttons on the analysis toolbar

to access these different procedures.

Summary Statistics for NORMAL

Count = 50

Average = 3,04952

Median = 2,80785

Mode =

Geometric mean = 2,85064

Variance = 1,32164

Standard deviation = 1,14963

Standard error = 0,162582

Minimum = 1,49722

Maximum = 5,8264

Range = 4,32918

Lower quartile = 2,09368

Upper quartile = 3,65679

Interquartile range = 1,56311

Skewness = 0,759567

Stnd. skewness = 2,19268

Kurtosis = -0,0765818

Stnd. kurtosis = -0,110536

Coeff. of variation = 37,6986%

Sum = 152,476

The StatAdvisor

--------------This table shows summary statistics for NORMAL.  It includes

measures of central tendency, measures of variability, and measures of

shape.  Of particular interest here are the standardized skewness and

standardized kurtosis, which can be used to determine whether the

sample comes from a normal distribution.  Values of these statistics

outside the range of -2 to +2 indicate significant departures from

normality, which would tend to invalidate any statistical test

regarding the standard deviation.  In this case, the standardized

skewness value is not within the range expected for data from a normal

distribution.  The standardized kurtosis value is within the range

expected for data from a normal distribution.

Hypothesis Tests for NORMAL

Sample mean = 3,04952

Sample median = 2,80785

t-test

-----Null hypothesis: mean = 3,0

Alternative: not equal

Computed t statistic = 0,304558

P-Value = 0,761992

Do not reject the null hypothesis for alpha = 0,1.

sign test

--------Null hypothesis: median = 3,0

Alternative: not equal

Number of values below hypothesized median: 28

Number of values above hypothesized median: 22

Large sample test statistic = 0,707107 (continuity correction applied)

P-Value = 0,479498

Do not reject the null hypothesis for alpha = 0,1.

signed rank test

---------------Null hypothesis: median = 3,0

Alternative: not equal

Average rank of values below hypothesized median: 24,0

Average rank of values above hypothesized median: 27,4091

Large sample test statistic = 0,328211 (continuity correction applied)

P-Value = 0,742748

Do not reject the null hypothesis for alpha = 0,1.

The StatAdvisor

--------------This pane displays the results of three tests concerning the center

of the population from which the sample of NORMAL comes.  The first

test is a t-test of the null hypothesis that the mean NORMAL equals

3,0 versus the alternative hypothesis that the mean NORMAL is not

equal to 3,0.  Since the P-value for this test is greater than or

equal to 0,1, we cannot reject the null hypothesis at the 90,0%

confidence level.  The second test is a sign test of the null

hypothesis that the median NORMAL equals 3,0 versus the alternative

hypothesis that the median NORMAL is not equal to 3,0.  It is based on

counting the number of values above and below the hypothesized median.

Since the P-value for this test is greater than or equal to 0,1, we

cannot reject the null hypothesis at the 90,0% confidence level.  The

third test is a signed rank test of the null hypothesis that the

median NORMAL equals 3,0 versus the alternative hypothesis that the

median NORMAL is not equal to 3,0.  It is based on comparing the

average ranks of values above and below the hypothesized median.

Since the P-value for this test is greater than or equal to 0,1, we

cannot reject the null hypothesis at the 90,0% confidence level.  The

sign and signed rank tests are less sensitive to the presence of

outliers but are somewhat less powerful than the t-test if the data

all come from a single normal distribution.

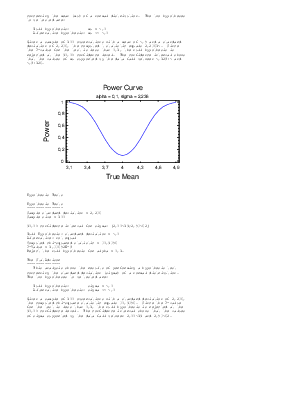
Hypothesis Tests

Hypothesis Tests

---------------Sample mean = 4,5

Sample standard deviation = 2,236

Sample size = 100

90,0% confidence interval for mean: 4,5 +/- 0,371264   [4,12874;4,87126]

Null Hypothesis: mean = 4,0

Alternative: not equal

Computed t statistic = 2,23614

P-Value = 0,0275879

Reject the null hypothesis for alpha = 0,1.

The StatAdvisor

--------------This analysis shows the results of performing a hypothesis test

concerning the mean (mu) of a normal distribution.  The two hypotheses

to be tested are:

Null hypothesis:        mu = 4,0

Alternative hypothesis: mu <> 4,0

Given a sample of 100 observations with a mean of 4,5 and a standard

deviation of 2,236, the computed t statistic equals 2,23614.  Since

the P-value for the test is less than 0,1, the null hypothesis