The results of performing a hypothesis test concerning the ratio of the standard deviations (sigma1/sigma2) of two samples from normal distributions

Hypothesis Tests

Hypothesis Tests

---------------Sample standard deviations = 2,63268 and 3,51617

Sample sizes = 50 and 100

95,0% confidence interval for ratio of variances: [0,350951;0,932736]

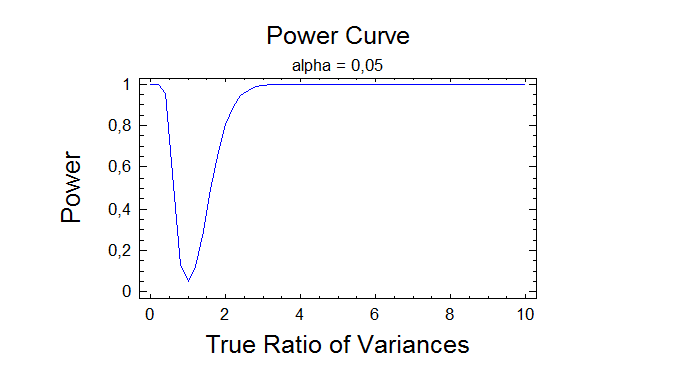
Null Hypothesis: ratio of variances = 1,0

Alternative: not equal

Computed F statistic = 0,560604

P-Value = 0,0263784

Reject the null hypothesis for alpha = 0,05.

The StatAdvisor

--------------This analysis shows the results of performing a hypothesis test

concerning the ratio of the standard deviations (sigma1/sigma2) of two

samples from normal distributions.  The two hypotheses to be tested

are:

Null hypothesis:        sigma1/sigma2 = 1,0

Alternative hypothesis: sigma1/sigma2 <> 1,0

Given one sample of 50 observations with a standard deviation of

2,63268 and a second sample of 100 observations with a standard

deviation of 3,51617, the computed F statistic equals 0,560604.  Since

the P-value for the test is less than 0,05, the null hypothesis is

rejected at the 95,0% confidence level.  The confidence interval shows

that the values of sigma1/sigma2 supported by the data fall between

0,350951 and 0,932736.

Hypothesis Tests

Hypothesis Tests

---------------Sample means = 7,29358 and 6,79665

Sample standard deviations = 2,63268 and 3,51617

Sample sizes = 50 and 100

Approximate 95,0% confidence interval for difference between means: 0,49693 +/- 1,01346   [-0,516531;1,51039]

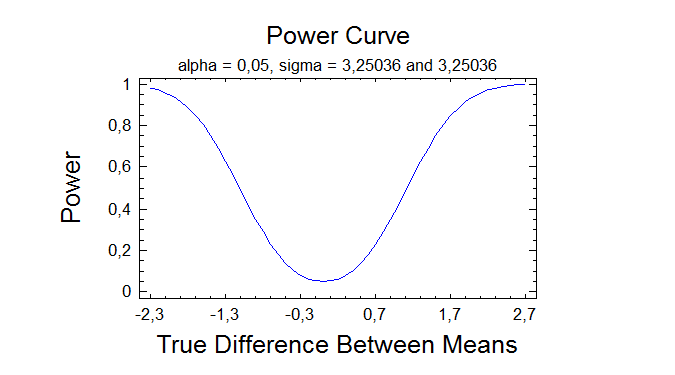
Null Hypothesis: difference between means = 0,0

Alternative: not equal

Computed t statistic = 0,970362

P-Value = 0,333728

Do not reject the null hypothesis for alpha = 0,05.

(Equal variances not assumed).

The StatAdvisor

--------------This analysis shows the results of performing a hypothesis test

concerning the difference between the means (mu1-mu2) of two samples

from normal distributions.  The two hypotheses to be tested are:

Null hypothesis:        mu1-mu2 = 0,0

Alternative hypothesis: mu1-mu2 <> 0,0

Given one sample of 50 observations with a mean of 7,29358 and a

standard deviation of 2,63268 and a second sample of 100 observations

with a mean of 6,79665 and a standard deviation of 3,51617, the

computed t statistic equals 0,970362.  Since the P-value for the test

is greater than or equal to 0,05, the null hypothesis cannot be

rejected at the 95,0% confidence level.  The confidence interval shows

that the values of mu1-mu2 supported by the data fall between

-0,516531 and 1,51039.

NOTE: in running this test, it has not been assumed that the

standard deviations of the two samples are equal.  You can make that

assumption by pressing the alternate mouse button and selecting

Analysis Options.

Multiple-Variable Analysis

Analysis Summary

Data variables:

NORM

NORM1

All available data will be used in each calculation.

The StatAdvisor

--------------This procedure is designed to summarize several columns of

quantitative data.  It will calculate various statistics, including

correlations, covariances, and partial correlations.  Also included in

the procedure are a number of multivariate graphs, which give

interesting views into the data.  Use the Tabular Options and

Graphical Options buttons on the analysis toolbar to access these

different procedures.

After this procedure, you may wish to select another procedure to

build a statistical model for your data.  Depending on your goal, one

of several procedures may be appropriate.  Following is a list of

goals with an indication of which procedure would be appropriate:

GOAL: build a model for predicting one variable given values of one of

more other variables.

PROCEDURE: Relate - Multiple regression

GOAL: group rows of data with similar characteristics.

PROCEDURE: Special - Multivariate Methods - Cluster Analysis

GOAL: develop a method for predicting which of several groups new rows

belong to.

PROCEDURE: Special - Multivariate Methods - Discriminant Analysis

GOAL: reduce the number of columns to a small set of meaningful

measures.

PROCEDURE: Special - Multivariate Methods - Factor Analysis

GOAL: determine which combinations of the columns determine most of

the variability in your data.

PROCEDURE: Special - Multivariate Methods - Principal Components

GOAL: find combinations of the columns which are strongly related to

each other.

PROCEDURE: Special - Multivariate Methods - Canonical Correlations

Summary Statistics

NORM                NORM1              

---------------------------------------------------------------------------------------------------Count               50                  100                

Average             7,29358             6,79665            

Variance            6,93102             12,3423            

Standard deviation  2,63268             3,51317            

Minimum             0,906411            -0,662894          

Maximum             14,551              17,3009            

Range               13,6446             17,9638            

Stnd. skewness      1,04745             1,25159            

Stnd. kurtosis      0,502824            0,0149142          

---------------------------------------------------------------------------------------------------The StatAdvisor

--------------This table shows summary statistics for each of the selected data