Сегнетоэластик в поле низкочастотной волны без учета пространственной дисперсии, страница 3

Вначале проанализируем наиболее распространенную схему опыта: будем считать, что при E_i0    Х_n = 0, а при Х_n 0   E_i = 0, т.е. электрическое и механическое воздействия не присутствуют одновременно. Будем исходить из выражения типа (2.45). Разложение (2.45) соответствует свободному кристаллу (см. условие (2.50)), поэтому его следует дополнить слагаемыми, характеризующими взаимодействие параметра перехода с обобщенной термодинамической силой Y_n. Здесь в роли Y_n выступает либо компонента вектора напряженности внешнего электрического поля E_i , либо компонента тензора механических напряжений Х_n. В обоих случаях трансформационные свойства g и Y_n различны, и от (2.45) можно перейти к разложению вида:

F = F₀ + ag²/2 + bg⁴/4 - z_n g²Y_n²   ,                       (4.70)

где z_n – константы.  Компоненты E_i и Х_n  при любых i и n  входят в это выражение одинаковым образом, что позволяет формально ввести параметр .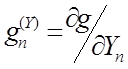

Используя (4.70), нетрудно выразить равновесное значение параметра перехода:

g = [a_T (T_Y -T)/b]^1/2, TT_Y  ;

(4.71)

g = 0, T >T_Y  ,      

где

T_Y = T_c+ z_nY_n²/a_T   .                                                (4.72)

Отсюда

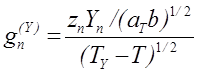  ,  TT_Y ;

(4.73)

= 0,   T >T_Y ,                     где Y_n E_i  либо Y_n   Х_n  .

Обратимся теперь к случаю, когда E_i и Х_n   воздействуют на кристалл одновременно. Интерес к такой нетрадиционной схеме опыта обусловлен тем, что определенные комбинации E_i и Х_n способны “переключать” домены кристалла в гиротропной фазе [84, 98]. Это означает, что те или иные комбинации E_i и Х_n , определяемые точечной симметрией кристалла, выступят в роли обобщенной термодинамической силы Г, сопряженной параметру g (см. формулу  (2.46)). В этом случае разложение (2.45) следует дополнить слагаемым, учитывающим взаимодействие параметра g с сопряженной ему величиной Г. Тогда вместо (2.45) имеем:

F=F₀ + ag²/2 + bg⁴/4 - z^*g Г.                                 (4.74)

Здесь z^* - константа взаимодействия параметра g с силой Г . Используя (4.74), получаем:

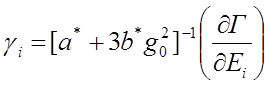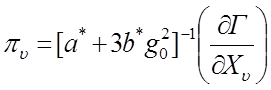,  ,          (4.75)

где a^*=a/z^*,

b^*=b/z^*,

g₀ – корень уравнения типа (4.8):

a^*g₀ + b^*g₀³ - Г= 0 .

Воспользуемся результатами проведенного в разд.4.2 анализа уравнения (4.8). Если Г велико  (Г>>a^*),  то в широкой окрестности точки ФП    (0<|T-T_c|/T_c1)  

g₀  (Г/b^*)^1/3, и температурную зависимость g₀ , g_i и p_n можно не учитывать. Если же Г не слишком велико, то в окрестности T_c функция g₀(T) испытывает влияние размывания ФП, которое наиболее существенно в непосредственной близости от T_c, где

|a*| = (a_T/z*)|T-T_c|<< Г.                                (4.76)

Вне этой области

g₀[a_T(T_c -T)/b]^1/2,   T<T_c   ;

g₀0,   T>T_c .

Тогда при T<T_c

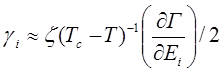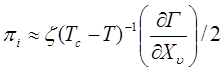,             ,         (4.77)

а при T>T_c

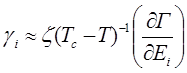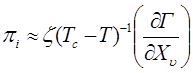,  ,                     (4.78)

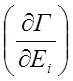где = z*/а_Т.  Выражения для  и 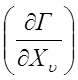 для различных гиротропных ФП приведены в табл. 4.1.

Таблица 4.1.

Обобщенные термодинамические силы  при гиротропных ФП

Гиротропный переход
m323	, =4,5,6	, ==4,5,6
6/mmm622, 4mm4, 6mm6, 4/mmm422, m232	X4 = X5 , i=1,2	E1=E2 , =4,5
4/mmm2m, 4/m	X4=X5 , i=1,2;  X6  , i=3	E1=E2 , =4,5; E3 , =6
mmm222	X4 , i=1;  X5 , i=2;  X6 , i=3	E1 , =4; E2 , =5; E3 , =6
m32, 3m3	X4=X5 , i=1; X5=X6 , i=2	E1 , =4,5; E2 , =6

Сравним (4.77) и (4.78) с формулой (4.73).  Из (4.73) следует, что при неодновременном воздействии E  и  X величины электрогирационного и пьезогирационного коэффициентов в низкосимметричной фазе резко возрастают по мере приближения к точке ФП (,  ~ (T_Y - T)^-1/2 ) и обладают слабой нелинейной зависимостью от Y_n . В высокосимметричной фазе = 0 и  = 0. При этом температура гиротропного ФП не зависит от знака Y_n (формула (4.72)). В то же время, при одновременном действии E_i и Х_n  электрогирационный коэффициент  и пьезогирационный коэффициент  вне зоны размывания (4.76) подчиняются закону типа Кюри – Вейсса и линейно зависят от E_i и от Х_n.