Сегнетоэластик в поле низкочастотной волны без учета пространственной дисперсии, страница 2

r(Т) ®r_¥ = const .                                   (2.41)

Тогда целесообразно выбрать параметр g в виде

g = r / r_¥ .                                                  (2.42)

Если же высокотемпературная фаза нецентросимметрична, то при  Т > Т_с

r(Т) = r⁺» А + В(Т – Т_с),                                     (2.43)

где А и В  -  константы, причем для многих кристаллов В ®0. В данном случае  результатом ФП является не спонтанное возникновение оптического вращения, а только его резкое изменение (излом зависимости r(Т) при Т=Т_с). Поэтому функцию r⁺(Т) можно экстраполировать в низкотемпературную фазу, отождествляя ее с регулярной составляющей суммарного вращения r, на фоне которой в низкотемпературной фазе возникает аномальное приращение

Dr(Т) = êr(Т) – r⁺(Т) ê.

При этом  удобно выбрать

g = Dr(Т)/ r⁺(Т),                                          (2.44)

где r_¥ и r⁺ считаем известными. Возмущение состояния кристалла в области гиротропного ФП можно описать разложением типа (1.2):

F = F_o + ag²/2 + bg⁴/4 + cg⁶/6 + …                     (2.45)

Как видим, параметр g по сути является специфической термодинамической координатой кристалла,  величина

Г = ¶F /¶ g                                                   (2.46)

– обобщенной термодинамической силой, сопряженной координате g, а соотношение

Г = g(a + bg² + cg⁴ +…)                                                 (2.47)

служит уравнением состояния гиротропного кристалла в области структурного ФП.

Для расчета температурных зависимостей физических величин на основе подобных соотношений необходимо, руководствуясь спецификой задачи, принять определенный априорный вид зависимостей коэффициентов а, b, с,… от температуры и внешних полей. Такой подход имеет ряд преимуществ, и мы вернемся к нему в главе 4. Здесь же мы не будем опираться на какую–либо частную форму уравнения состояния Г=Г(g) типа (2.47) и ограничимся наиболее общим предположением. Будем считать, что существует аналитическая функция

Г = Г(g, t, Y),        где t = (Т – Т_с) / Т_с,

Y – обобщенная термодинамическая сила, не сопряженная параметру перехода, и что эта функция представима в виде

Г = g f(t, g^Z, Y^D),                                          (2.48)

где f(t, g^Z, Y^D) – однородная функция переменных t, g^Z, Y^D,

Z и D – критические показатели.

По определению, однородная функция степени x удовлетворяет равенству:

f(Qt, Qg^Z, QY^D) = Q^xf(t, g^Z, Y^D).                             (2.49)

Равновесное значение параметра перехода g = g_o, реализующееся в кристалле при заданных внешних условиях, соответствует минимуму термодинамического потенциала. Условие минимума ¶F/¶g = 0 эквивалентно требованию

Г = 0 .                                                (2.50)

Используя (2.49), (2.50), можно показать, что выбор уравнения состояния в форме (2.48) эквивалентен асимптотическим соотношениям

g_o = N_g t^1/Z,  g_o = R_gY^D/Z , g_o  = F_gГ^{1/(1+Z x)} ,   (¶ g/¶G) =N_Г t^-x  ,            (2.51)

где N_g, N_Г, R_g и F_g – константы.  Связь критических показателей Z, D и x с критическими показателями других оптических и термодинамических величин, рассмотренными выше, можно найти, воспользовавшись соотношением типа [116] для термогирационного коэффициента b_о = ¶g_o /¶T:

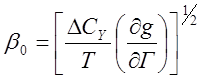          .                                           (2.52)

Вначале проанализируем поведение величины (¶G/¶ g).  Имеем:

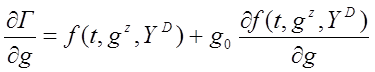            .                       (2.53)

Используя (2.49), (2.51), находим :

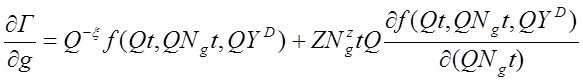   .               (2.54)

Параметр Q, по определению, может быть выбран произвольно. Если Y=const, то удобно выбрать Q = t ^–1. Тогда, возвращаясь к (2.52) и определяя для b_о критические показатели с помощью соотношений  b_о = (N_g /Z) t^{1/Z -1},    b_o = R_b Y ^y, с учетом (2.51) получаем :

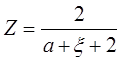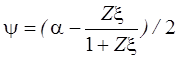,           .(2.55)

Первое сообщение [82] об экспериментальном наблюдении гиротропного ФП появилось достаточно давно. Однако за прошедшие два десятилетия попытка теоретического исследования этого явления была предпринята только в работе [98], где были выявлены некоторые качественные закономерности гиротропных ФП и дана их классификация. Отдельные аспекты обсуждаемой проблемы затрагивались также в [84]. Здесь мы проанализируем возможность количественного описания температурного поведения электрогирационного коэффициента  g_i = ¶g/¶E_i и пьезогирационного коэффициента p_n = ¶g/¶ X_n   при гиротропных ФП.