Сложность ГПС в значительной мере затрудняет формирование единого подхода к проектированию и внедрению, который определяется различием ТП, типом производства, специфики подходов и накопленного опыта проектирования в разных отраслях промышленности. Можно предположить, что в дальнейшем будут развиваться различные концепции создания ГПС.
Появление новых технологий, средств производства и материалов, более совершенных методов и форм организации труда, динамика изменения спроса являются объективными предпосылками для развития ГПС. Поэтому ГПС должны создаваться в соответствии с концепцией развивающихся систем. Следовательно, возникает объективная необходимость в системном подходе к разработке долгосрочной стратегии развития ГПС по приоритетным направлениям как для предприятий, так и отраслей народного хозяйства. При выборе путей развития ГПС необходима разработка научно обоснованных методов прогнозирования.
Проблема научно-технического прогнозирования сводится к построению многовариантной гипотезы о возможных результатах и путях развития ГПС и различает изыскательское и нормативное прогнозирование.
Изыскательское прогнозирование изучает в рамках заданного интервала времени изменение причинно-следственных связей и возможностей развития ГПС от настоящего времени к будущему.
Нормативное прогнозирование определяет сначала будущие цели или потребности, а затем исследует возможные пути их достижения, т.е. прослеживается картина развития от будущего к настоящему. Часто оба вида прогнозирования используют совместно в интерактивном режиме.
В настоящее время разработано более ста различных методов научно-технического прогнозирования [15,18] . Важнейшей характеристикой их является временной интервал (горизонт) прогнозирования. Наиболее эффектнвным считается научно-техническое прогнозирование на 15 лет. Это средний срок "инкубационного" состояния научных открытий, после чего находятся технологические решения их реализации.
Долгосрочные прогнозы нужны для выработки научно-технической политики отрасли и народного хозяйства. К наиболее известным методам научно-технического прогнозирования можно отнести методы экстраполяции, экспертных оценок, морфологического расчленения, моделирования (логические, информационные, имитационные, игровые и т.д.), сценариев анализа деревьев целей.
1.6. Модель развития ГПС на основе корреляционного анализа
Прогнозирование характеристик элементов ГПС позволяет определять правильный выбор оборудования с учетом его совершенствования и сократить моральный износ. Рассмотрим основные положения корреляционного анализа для прогнозирования количественных значений характеристик оборудования ГПС.
Корреляционно-регрессионный анализ дает возможность установить математическую зависимость между характеристиками оборудования ГПС и предусматривает решение следующих вопросов:
- какова форма связи между характеристиками оборудования (линейная, нелинейная);
- насколько тесна связь между характеристиками;
- каковы значения неизвестных коэффициентов, свободных членов и показателей степени характеристик математической модели;
- какова степень адекватности полученной модели.
Определение учитываемых факторов
Выбор учитываемых факторов является ответственным этапом, так как математический аппарат теории множественной корреляции может дать удовлетворительные результаты только при наличии причинно-следственных связей между ними. Включение в модель факторов, физическую природу которых нельзя объяснить ни логически, ни профессионально, приведет к ошибочной математической модели явления. При отборе факторов для включения в модель следует иметь в виду, что их количестве не должно быть слишком большим, так как иначе она будет громоздкой, малопригодной к практическому использованию, независимые факторы не должны находиться между собой в функциональной или близкой к ней связи. Если коэффициент парной корреляции между двумя независимыми факторами больше 0,8, то один из них, который имеет меньший коэффициент корреляции с зависимым фактором, следует исключить из анализа.
Составление уравнения регрессии
Уравнением регрессии в теория математической статистики называется уравнение, устанавливающее связь между зависимыми и независимыми переменными (факторами). Если связь определяется для трех и более переменных, она называется уравнением множественной регрессии. Зависимость исследуемой переменной от независимых факторов может иметь линейный или криволинейный закон. Линейная зависимость выражается уравнением более простого вида. Учитывая это, нелинейные зависимости стремятся привести к линейному виду. Приведение криволинейных зависимостей к линейному виду для упрощения расчетов обычно производится посредством их выражения в логарифмическом виде. Используя этот прием, рассмотрим линейный вид уравнения множественной регрессии
![]() , (1)
, (1)
где Т - зависимая
переменная; X ,Y,..., К - независимые переменян; ![]() - свободный член;
- свободный член; ![]() - коэффициенты независимых
переменных.
- коэффициенты независимых
переменных.
В общем случае зависимость прогнозируемого показателя от независимых переменных можно считать нелинейной и выразить с определенной степенью точности в виде степенного уравнения вида
![]() , (2)
, (2)
которое после логарифмирования приводится к линейному виду
![]() .
(3)
.
(3)
Методика определения коэффициентов уравнений (1) и (3) одинакова. Для получения расчетной формулы вида (2) после получения коэффициентов уравнения (3) производится потенцирование.
Методика определения коэффициентов множественной регрессии
Установить среднее арифметическое значение учитываемых независимых факторов
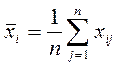 ,
(4)
,
(4)
где ![]() -
число (объем) статической выборки.
-
число (объем) статической выборки.
Определить отклонение каждого ![]() -го значения от среднеарифметического
-го значения от среднеарифметического
![]() .
(5)
.
(5)
Определить значения среднеквадратичных отклонений учитываемых факторов, которые характеризует рассеивание относительно среднего значения
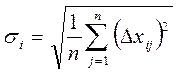 .
(6)
.
(6)
Вычислить коэффициент вариации для каждого учитываемого фактора
![]() .
(7)
.
(7)
Установлено, что при ![]() , применение статистических методов
в рассматриваемом случае является вполне корректным.
, применение статистических методов
в рассматриваемом случае является вполне корректным.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.