Усилие на валы направлено
по линии центров передачи и в любом случае ![]() :
:
![]()
Основные параметры шкивов приведены в таблице:
|
Параметр |
Обозн. |
Расчетная формула |
Значение |
||
|
1 |
2 |
||||
|
Модуль зацепления, мм |
т |
|
5 |
||
|
Число зубьев |
z |
- |
20 |
28 |
|
|
Диаметр вершин зубьев, мм |
da |
|
98 |
138 |
|
|
Диаметр впадин, мм |
df |
|
89 |
129 |
|
|
Высота зуба, мм |
hш |
|
4,5 |
||
|
Диаметр условной окружности измерения, мм |
dу |
|
94 |
134 |
|
|
Угол впадины, град. |
2 |
|
- |
||
|
Окружной шаг по условной окружности измерения, мм |
ty |
|
14,8 |
15 |
|
|
Толщина зуба по дуге условной окружности измерения |
Sy |
|
8 |
8,2 |
|
|
Радиус закругления головки зуба, мм |
rr |
|
1,75 |
||
|
Радиус закругления ножки зуба, мм |
rn |
|
2 |
||
|
Длина зуба, мм |
B |
|
37 |
||
Трансмиссионный вал: ( рис.4.5 ) Исходные данные к расчетам:
![]()
![]() -
сила, действующая на вал от натяжения ремня:
-
сила, действующая на вал от натяжения ремня:
![]()
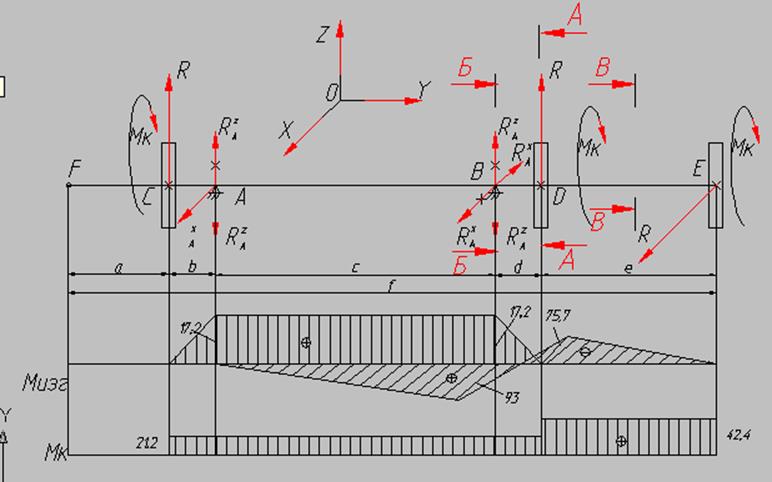 |
Определение реакций в точке В:
в плоскости ZOY:
![]()
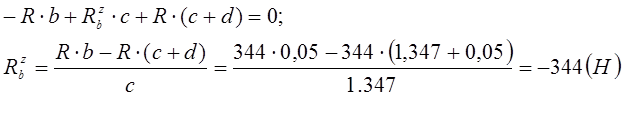
в плоскости XOY:
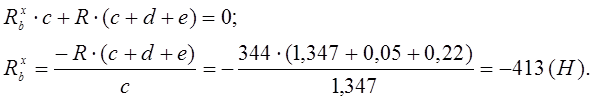
Суммарная реакция в точке B:
![]()
![]() Определение реакций в точке A:
Определение реакций в точке A:
![]() в плоскости ZOY:
в плоскости ZOY:![]()
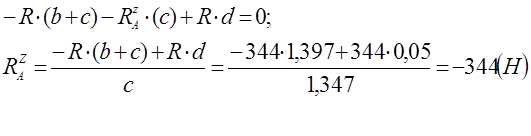
в плоскости XOY:
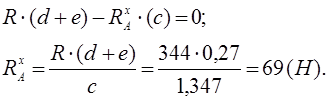
Суммарная реакция в точке A:
![]()
Проверка:
Сумма всех сил на ось Z:
![]()
Сумма всех сил на ось X:
![]() .
.
Эпюра изгибающих моментов в плоскости XOY (рис 4.5):
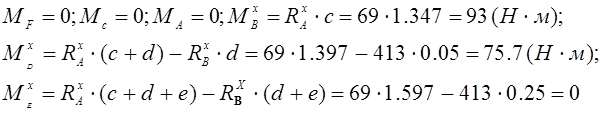
Эпюра изгибающих моментов в плоскости
ZOY (рис 4.5)
: 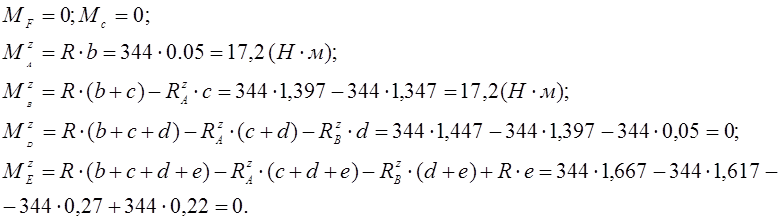 Эпюра крутящих моментов:
Эпюра крутящих моментов:
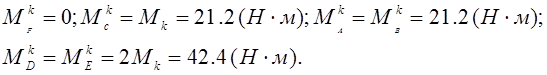
Примем , что нормальные напряжения от изгиба изменяются по симметрич-ному циклу, а касательные от кручения – по отнулевому (пульсирующему).
Уточнённый расчёт состоит в определении коэффициентов запаса прочнос-ти s для опасных сечений и сравнении их с требуемыми (допускаемыми) значени-ями [s].
Трансмиссионный вал (рис.3.4.1 ).
Материал вала Сталь 45, термическая обработка – улучшение.
Среднее значение sВ=780 Мпа.
Предел выносливости при симметричном цикле изгиба:
s-1=![]()
Предел выносливости при симметричном цикле касательных напряжений:
t-1=![]()
Сечение А – А . Это сечение при передаче вращающего момента от трансмиссионнго вала к валу ротора, рассчитываем на кручение. Концентрацию напряжений вызывает наличие шпоночной канавки.
Коэффициент запаса прочности:
![]()
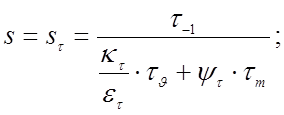 (4.21)
(4.21)
где амплитуда и среднее напряжение отнулевого цикла:
![]()
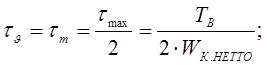 (4.22)
(4.22)
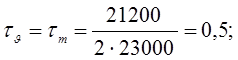 |
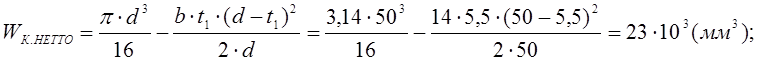
Принимаем ![]() ([2], табл. 8.5),
([2], табл. 8.5), ![]() ([2], табл. 8.8) и
([2], табл. 8.8) и ![]() ([2], с. 166).
([2], с. 166).
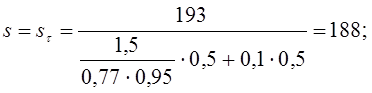
Момент сопротивления изгибу:
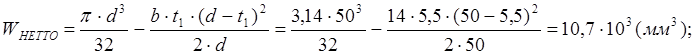
Момент изгибающий:
![]()
![]()
Амплитуда нормальных напряжений изгиба:
![]()
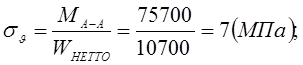
Коэффициент запас прочности по нормальным напряжениям:
![]()
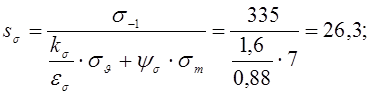
где ![]() ([2], табл. 8.5),
([2], табл. 8.5), ![]() ([2], табл. 8.8) и
([2], табл. 8.8) и ![]() ([2], с. 166).
([2], с. 166).
Результирующий коэффициент запаса прочности:
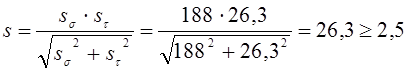 ;
;
Сечение Б –Б.
Концентрация напряжений обусловлена посадкой подшипника в опоре В с
гарантированным натягом. Принимаем ![]()
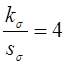 и
и 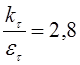 , принимаем
, принимаем ![]() и
и ![]() ([2], с. 166).
([2], с. 166).
Изгибающий момент (рис.4.5 ):
![]()
![]()
Осевой момент сопротивления:
![]()
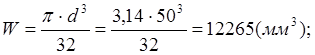
Амплитуда нормальных напряжений:
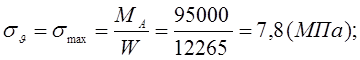
![]()
Полярный момент сопротивления:
![]()
Амплитуда и среднее напряжение цикла касательных напряжений:
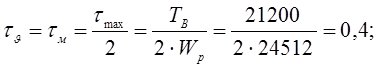
Коэффициент запаса прочности по нормальным напряжениям:
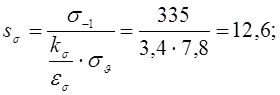
Коэффициент запаса прочности по касательным напряжениям:
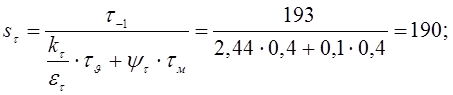
Результирующий коэффициент запаса прочности для сечения Б-Б:
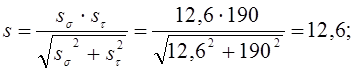
Сечение В – В. Концентрация напряжения обусловлена
переходом от Æ 50 мм к Æ 40 мм: при 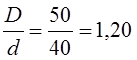 и
и
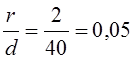 коэффициенты концентрации нап-ряжений
коэффициенты концентрации нап-ряжений![]() и
и ![]() ([2], табл. 8.2). Масштабные факторы
([2], табл. 8.2). Масштабные факторы ![]() и
и ![]() ([2], табл. 8.8).
([2], табл. 8.8).
Осевой момент сопротивления:
![]()
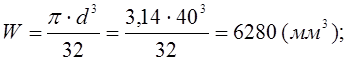
Амплитуда нормальных напряжений:
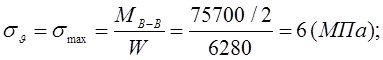
![]()
Полярный момент сопротивления:
![]()
Амплитуда и среднее напряжение цикла касательных напряжений:
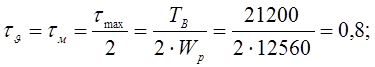
Коэффициент запаса прочности по нормальным напряжениям:
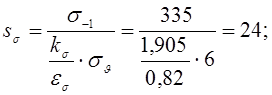
Коэффициент запаса прочности по касательным напряжениям:
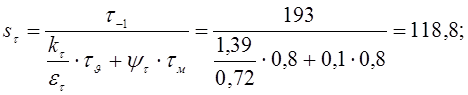
Результирующий коэффициент запаса прочности для сечения В-В:
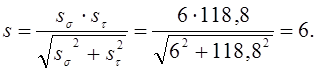
Шарикоподшипник радиальный сферический двухрядный ГОСТ 572-75: D=90 мм, В=20 мм, C=22,9 кН, С 0=10,8 кН.
Для данного подшипника эквивалентная нагрузка рассчитывается по формуле:
![]() (4.23)
(4.23)
где V- коэффициент, при вращении внутреннего кольца V=1;
Fr-
радиальная нагрузка, ![]() - реакция в подшипнике;
- реакция в подшипнике;
Расчётная долговечность:
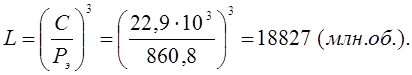 (4.24)
(4.24)
Номинальная долговечность:
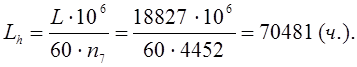 (4.25)
(4.25)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.