


ИССЛЕДОВАНИЕ МАТЕМАТИЧЕСКОЙ МОДЕЛИ
Тело массой т подвешено к концу пружины с коэффициентом жесткости С и помещено в жидкость (рис. 3.1). В начальный момент груз из положения статического равновесия смещен в заданном направлении на величину хО (таб. 3.1) и ему в заданном направлении сообщена начальная скорость VО. В процессе движения на тело так же действует возмущающая сила Р(t) заданная кусочно-непрерывной функцией, (рис. 3.2 а) параметры которой приведены в таблице 3.2. Сила сопротивление движению R пропорциональна скорости тела R( V ) =-bV
где b - коэффициент сопротивления жидкости в зависимости от глубины, задан графически (рис. 3.2 б), коэффициент сопротивления воздуха b0=5
Вариант 15
M=35кг; V0=6м/с; X0=0.08м; C=2500H/м; h=0.12м; h1=0.6м
Параметры возмущающей силы Р(t)
t1=1c; t2=2c; t3=5c; P0(t)=100*sin(wt), H ; P1(t)=200*sin(2wt), H ; P2(t)=10*cos(2wt)*50*sin(3wt), H; P3(t)=0 , H;
где t1,t2,t3 моменты времени изменения силы Р(t). (t0=0).
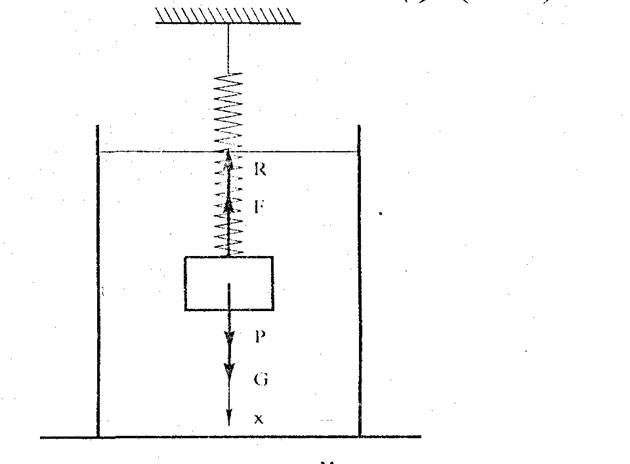
Схема движения груза и действующие на него сил
Постановка задачи
1.Составить математическую модель колебательного движения груза под воздействием возмущающей силы P(t)
2. В пакете MathCAD по полученной математической модели определить значения функций движения, скорости и ускорения груза;
3. Построить графики функций движения, скорости и ускорения тела;
4. С помощью пакета MathConnex выполнить моделирование влияния коэффициента жесткости пружины (C) на движение груза и определить при какой предельной жесткости С1 груз не выйдет за допустимую глубину h1.
5. Для найденной жесткости пружины построить графики функций движения, скорости и ускорения груза.
Составление математической модели.
Направим ось х вдоль пружины по вертикали вниз, взяв начало отсчета в положении статического равновесия груза. Запишем начальные условия движения груза:
при t=0 x=x0 x’=x’0
Изобразим груз в положении, при котором его абсцисса х положительна.
Предположим, что груз движется в сторону возрастания абсциссы х.
Кроме сил F и R, кгрузу приложена его сила тяжести Р = тg. Составим дифференциальное уравнение движения груза:
mx’’+R(V)-F+G=P(t);
где G=mg- вес тела
F=-c(Δ-x)- сила упругости
При t=0, V=6, X0=0.08
2.3. Вычисление дифференциального уравнения в пакете MathCAD.
1. Составим математическую модель движения груза под воздействием
силы P(t).![]()
t1, t2, t3-моменты времени изменения силы P1, P2, P3 соответственно .
![]()
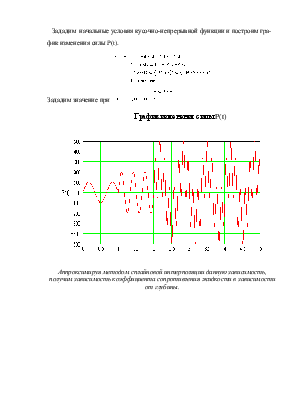
Зададим начальные условия кусочно-непрерывной функции и построим график изменения силы P(t).
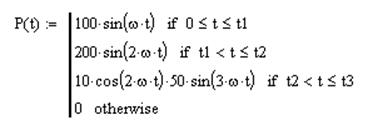
![]()
Зададим значение при ![]()
График изменения силы P(t)
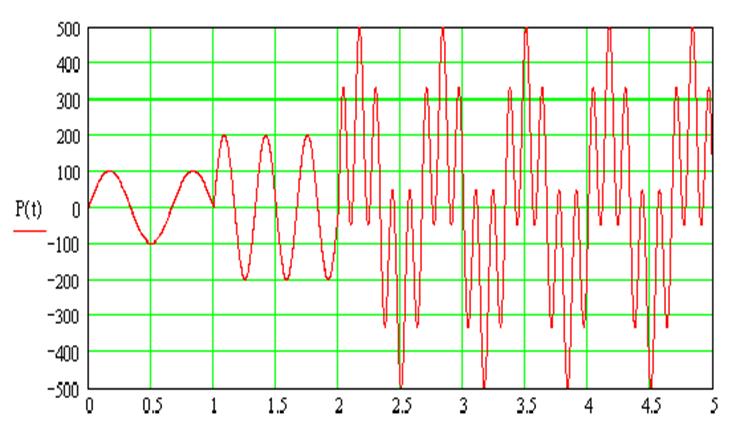
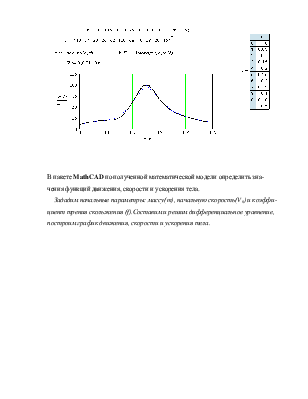
Аппроксимируя методом сплайновой интерполяции данную зависимость, получим зависимость коэффициента сопротивления жидкости в зависимости от глубины.
В пакете MathCAD по полученной математической модели определить значения функций движения, скорости и ускорения тела.
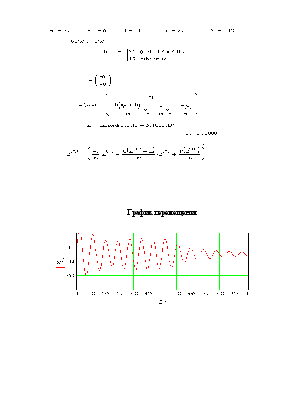
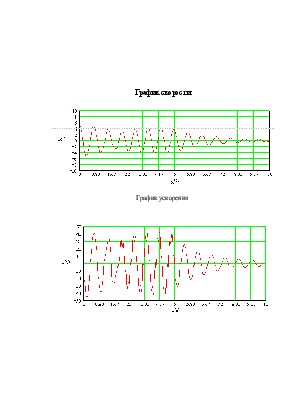
Зададим начальные параметры: массу(m), начальную скорость(V0) и коэффициент трения скольжения (f).Составим и решим дифференциальное уравнение, построим график движения, скорости и ускорения тела.

График перемещения
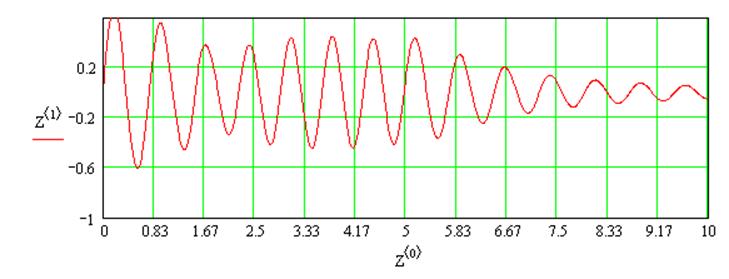
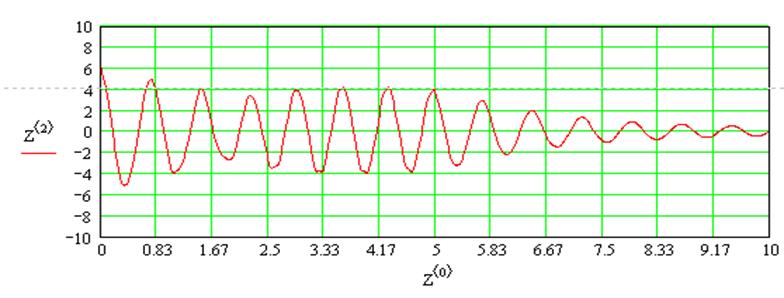
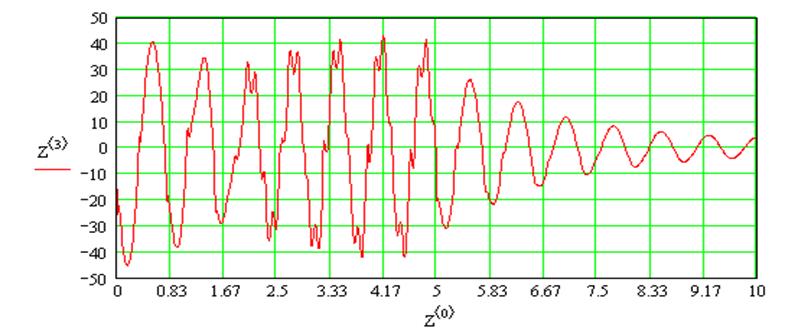
Следующее выражение необходимо нам для моделирования влияния коэфициента жесткости пружины (С) на движение груза и определения при какой предельной жесткости груз не выйдет на допустимую глубину
(с помощью пакета MathConnex)

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.