Моделирование на основе решения ДУ второго порядка
Моделирование линейного осциллятора
ДУ второго порядка принадлежит особая роль в науке и в технике — отчасти из-за того, что именно эти уравйения лежат в основе теории колебаний. Выше уже приводились примеры аналитического решения линейных ДУ второго порядка. Однако в большинстве случаев пользователей интересуют прежде всего графики решения таких ДУ. В этом случае, а также когда ДУ оказываются нелинейными, решение целесообразно выполнять численными методами.
Начнем с графической визуализации решения линейного ДУ второго порядка, ха-рактерного для так называемых осцилляторов — колебательных систем, создающих почти гармонические (или, точнее, ангармонические) колебания. На рис. 25.1 приведены результаты решения ДУ для типового осциллятора, характеризующе-гося двумя параметрами а и б, которые можно рассматривать как коэффициент затухания и частоту резонанса, соответственно. Для решения использованы блоки с функцией odesolve, включенной только в последние версии Mathcad 2000/2001.
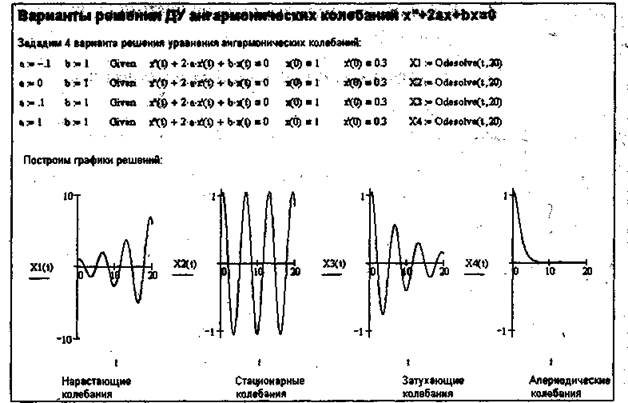
Рис. 25.1. Варианты решения ДУ второго порядка для осциллятора
Как видно из рис. 25.1, реализуются хорошо известные режимы работы осциллятора: нарастающих, стационарных, затухающих и апериодических колебаний.
Соотношения между параметрами а и bдля этого вида Д У хорошо известны из | теории колебаний и потому здесь не обсуждаются: Отметим лишь, что стащио-нарные колебания возможны при а =0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.