



Задание 3. Параметрический синтез и кинематический анализ передаточного механизма с использованием системы MathCad
1. С использованием системы MathCAD рассчитать длины звеньев кривошипно-ползунного механизма по заданным исходным данным. Проверить условие существования механизма.
2. Рассчитать функции координат характерных точек механизма в зависимости от угла поворота кривошипа. Построить графики этих функций.
3. Рассчитать функции аналогов скоростей и ускорений шатуна и ползуна в зависимости от угла поворота кривошипа. Построить графики этих функций.
4. Рассчитать функции проекций аналогов скоростей и ускорений в зависимости от угла поворота кривошипа. Построить графики этих функций.
5. Рассчитать функции хода ползуна в зависимости от угла поворота кривошипа. Построить график этой функций.
Исходными данными для работы являются:
φ1, φ2, φ3 – начальные значения угла поворота кривошипа
S1, S2, S3 – начальные значения перемещения ползуна
a4– длина звена механизма
β– угол между звеньями механизма
Таблица исходных данных
Таблица 3.1.
|
N варианта |
(град) |
(град) |
(град) |
S1 (м) |
S2 (м) |
S3 (м) |
a4 (м) |
Β (град) |
|
1 |
17 |
30 |
45 |
2,7 |
1,1 |
0,6 |
0,1 |
100 |
|
2 |
35 |
25 |
20 |
0,95 |
1,8 |
2,7 |
0.05 |
110 |
|
3 |
18 |
28 |
55 |
3,9 |
2,5 |
0,9 |
0,09 |
120 |
|
4 |
25 |
42 |
65 |
2,3 |
1,7 |
1,2 |
0,08 |
115 |
|
5 |
23 |
47 |
72 |
3.7 |
2.5 |
1,2 |
0,1 |
125 |
|
|
Описание математической модели
Дан кривошипно-ползунный механизм, исходными данными для проектирования которого служит функциональная зависимость перемещения ползуна S от угла поворота кривошипа φ. Необходимо определить длины звеньев a1, a2 и значение параметра a3. Значения a4и β заданы.
Таблица значений φi и Si может содержать по три значения, т.е. задаются три положения механизма (i=1,2,3). В этом случае, если удовлетворяется условие существования механизма
a1 < a2 - a3
то задача сводится к решению трех уравнений и имеет единственное решение.
При i=3 механизм описывается уравнением вида:
K1 Sicos φi + K2 sin φi – K3 = Si2
Длины звеньев вычисляются по формулам:
![]()
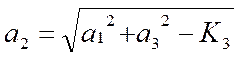
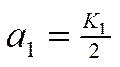
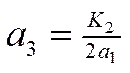
Ниже приведены соотношения для определения кинематических характеристик, координат, проекций аналогов скоростей и ускорений звеньев и точки N, закрепленной на шатуне.
Координаты точек С, В, N определяются по следующим выражениям:
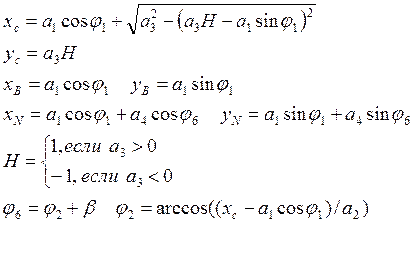
Аналоги угловой скорости и ускорения шатуна вычисляются по формулам:
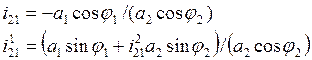
Для ползуна соотношения имеют вид:
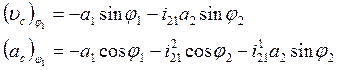
Проекции аналогов скоростей и ускорений точки N определяются из следующих выражений:
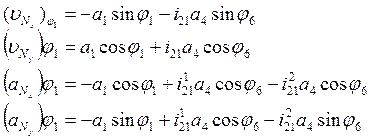
Ход ползуна определяется следующей формулой:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.