Исследование математической модели траектории полета тела брошенного под углом к горизонту

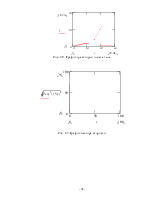
окончательные уравнения проекций всех сил на координатные оси:

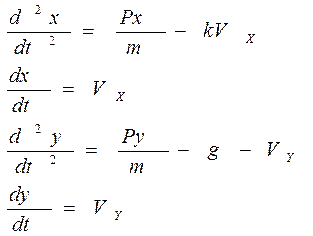
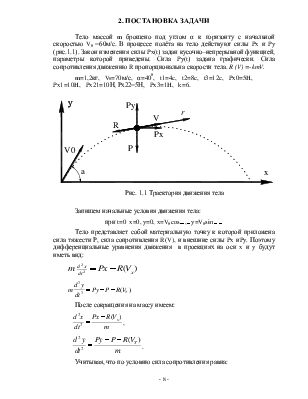
Данная система уравнений является математической моделью движения тела под действием совокупности всех сил действующих на него. Решив эту систему можно получить все интересующие на характеристики движения тела.

3. ИССЛЕДОВАНИЕ МАТКМАТИЧЕСКОЙ МОДЕЛИ В MATHCAD

Для того, чтобы исследовать математическую модель движения тела необходимо задать силы, действующие на тело в том виде, в котором они описаны в условии данной задачи. А именно: функция силы Px – кусочно-непрерывная функция, функция Py–непрерывная функция.

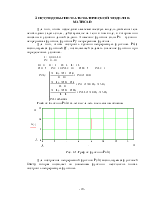
Для того, чтобы построить кусочно-непрерывную функцию Px(t) воспользуемся функцией if , позволяющей задавать значение функции при определенных условиях.

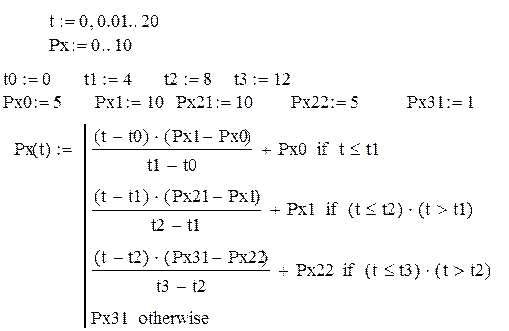
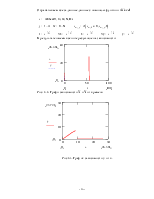
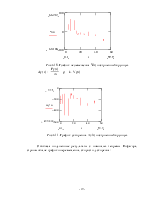
График функции Px(t) будет выглядеть следующим образом

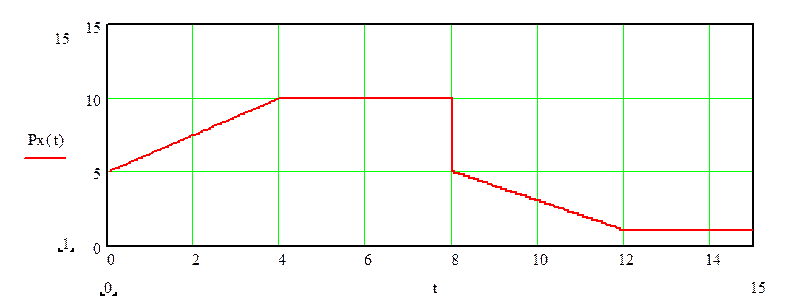
 Рис. 3.1. График функции Px(t)

Для построения непрерывной функции Py(t) воспользуемся функцией linterp, которая позволяет по значениям функции  нескольких точках построить непрерывную функцию.

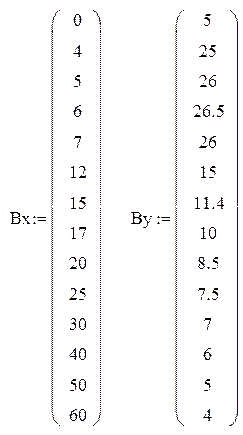
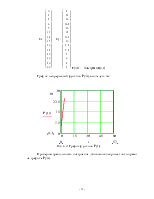
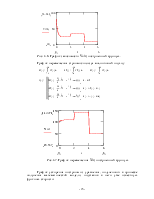
График непрерывной функции Py(t), выглядеть так

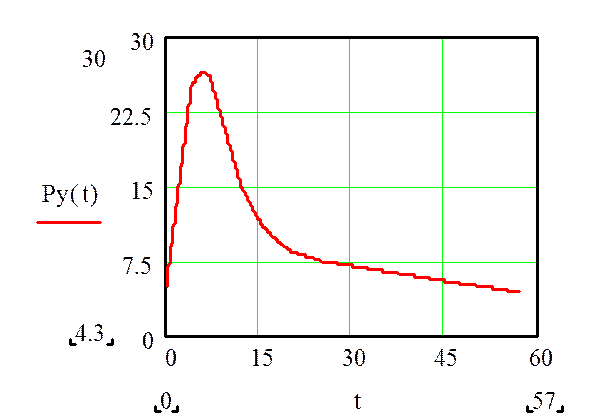
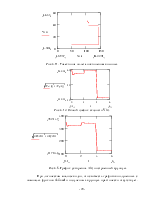
Рис. 3.2. График функции Py(t)

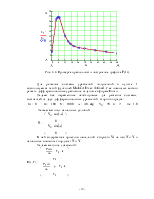
Проверим правильность построения ,обозначив опорные точки прямо на графике Py(t).

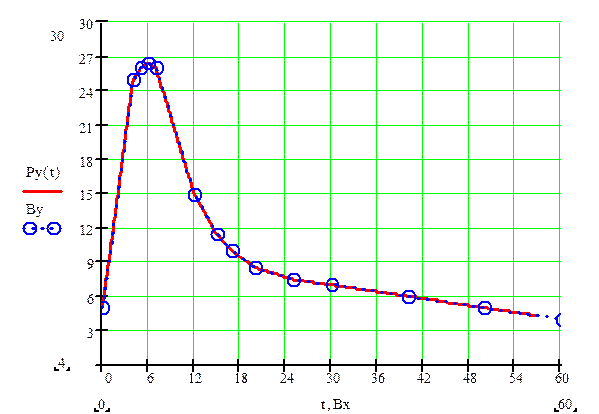
Рис. 3.3. Проверка правильности построения графика Py(t).

Для решения системы уравнений полученной в пункте 1 воспользуемся такой функцией MathCAD как rkfixed. С ее помощью можно решать дифференциальные уравнения, заданные в форме Коши.

Задаем все переменные необходимые для решения системы, состоящей из двух дифференциальных уравнений  второго порядка:

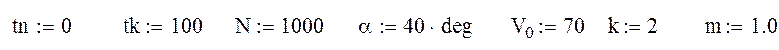
Задаем матрицу начальных условий:

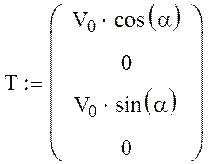
В ней содержаться проекции начальной  скорости V₀ на оси X и Y и начальные значения координат X и Y.

Задаем матрицу уравнений:

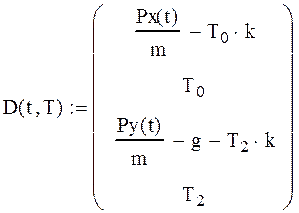
Обрабатываем все заданные данные с помощью функции rkfixed:

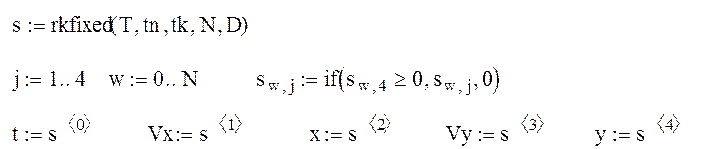
В результате имеем все интересующие на зависимости:

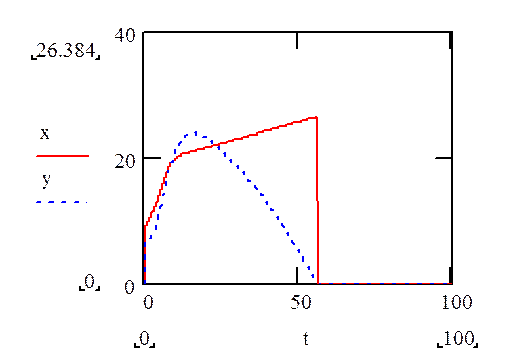
Рис. 3.3. Графи зависимости X и Y от времени

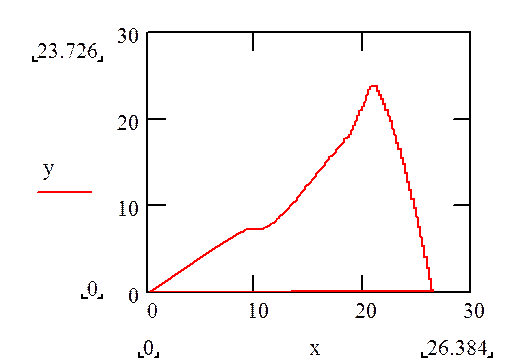
Рис3.4. График зависимости y от x.

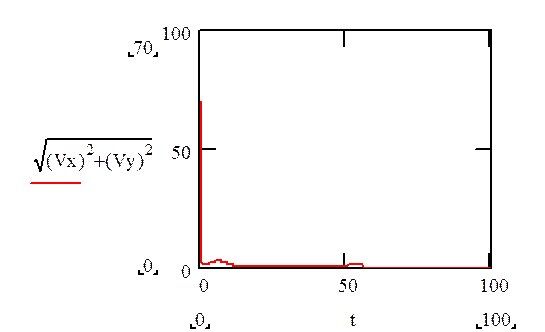
Рис.3.5. График зависимости скорости от времени

Данные, полученные с помощью функции rkfixed  можно сравнить с результатами, полученными при интегрировании вручную. Для этого рассмотрим в отдельности уравнения на оси X и Y. Но постольку, поскольку сила Px(t) задана отрезками, то проинтегрировать полностью все уравнение не удастся. Поэтому выведем в отдельности интеграл функции Px(t) и уравнения движения тела без воздействия на него посторонних сил, а потом сложим полученные результаты.

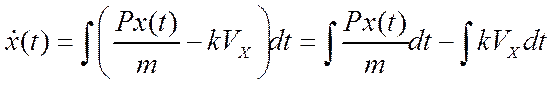
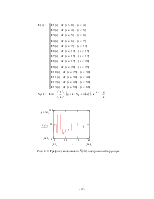
Интеграл функции будет состоять из кусочков и выглядит следующим образом:

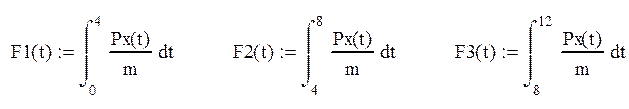
Опуская математические преобразования, укажем лишь значение второго интеграла:

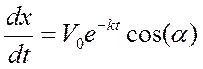
График вектора скорости построим из кусочков, воспользовавшись функцией if:

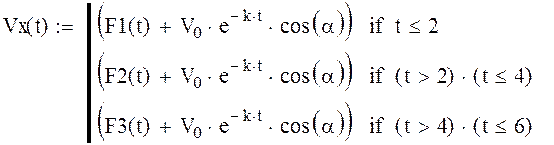
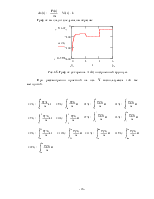
Полученный график будет иметь следующий вид:

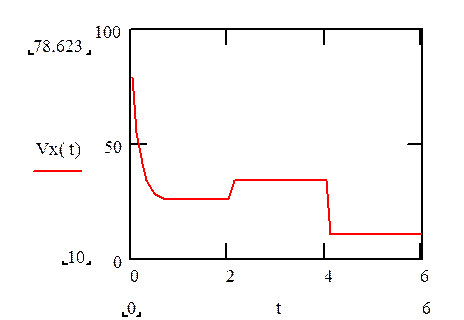
Рис. 3.6. График зависимости Vx(t) построенный вручную.

График перемещения строим используя аналогичный подход:

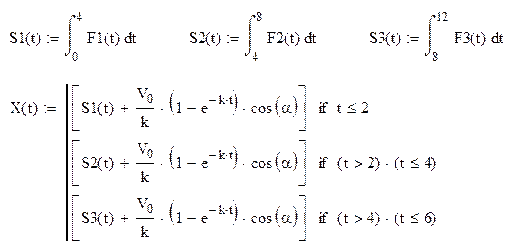
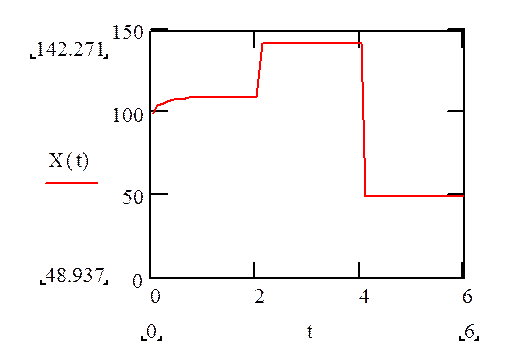
Рис.3.7. График перемещения X(t) построенный вручную

График ускорения построим из уравнения, полученного в процессе получения математической модели, подставив в него уже известную функцию скорости:

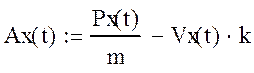
График выглядит следующим образом:

Рис.3.8. График ускорения. Аx(t) построенный вручную

При рассмотрении проекций на ось Y воспользуемся той же методикой.

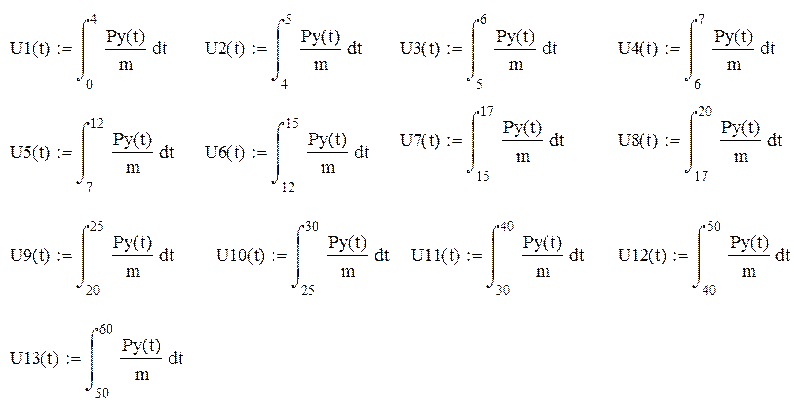
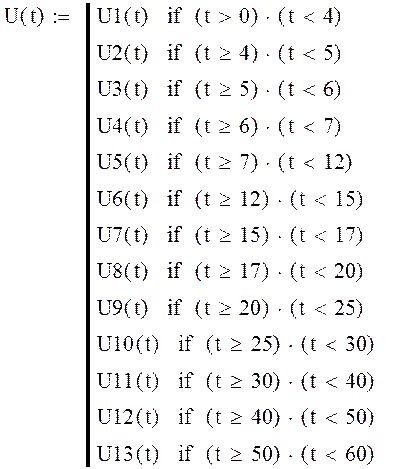
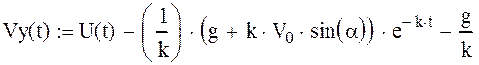
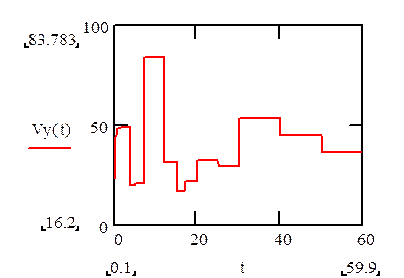
Рис. 3.9. График зависимости Vy(t) построенный вручную

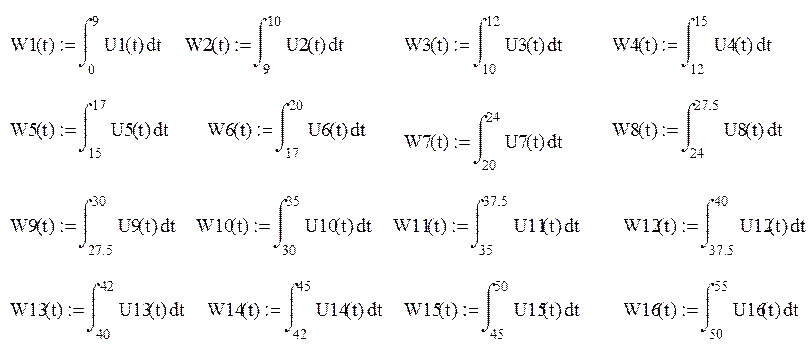
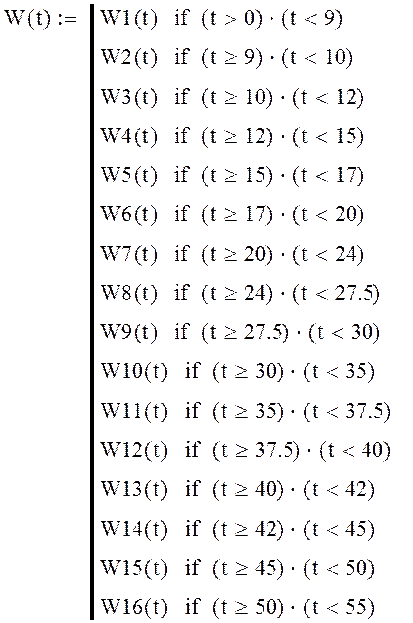
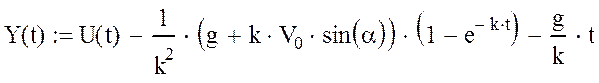
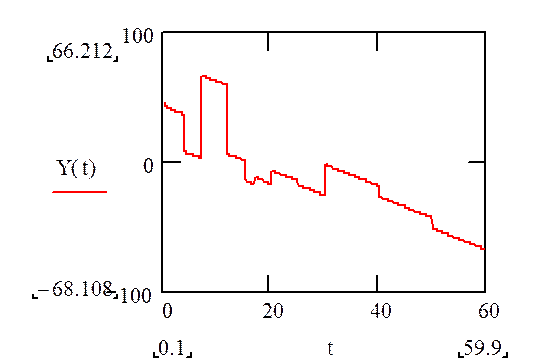
Рис.3.10. График перемещения Y(t) построенный вручную

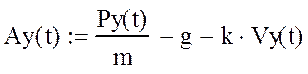
Рис.3.11. График ускорения. Аy(t) построенный вручную

Обобщая полученные результаты с помощью теоремы Пифагора, строим общие графики перемещения, скорости, ускорения:

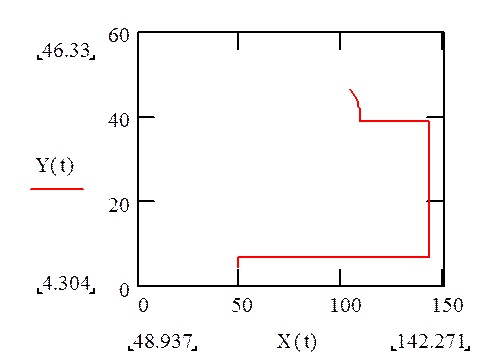
Рис.3.11. Траектория полета построенная вручную

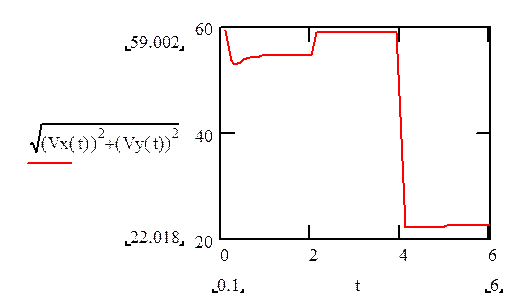
Рис.3.12. Общий график скорости V(t).

Рис.3.8. График ускорения. А(t) построенный вручную

При логическом анализе видно, что схожесть графиков полученных с помощью функции rkfixed и полученных вручную практически отсутствует. Отсюда можно сделать вывод, что погрешность расчетов произведенных вручную очень велика т.к. функцию заданную кусочно-непрерывно при помощи линии проинтегрировать не представляется возможным.    

С помощью приложения MathConnex выполним моделирование влияния угла   на траекторию движения и определим, при каком угле  тело пролетит наибольшее расстояние.

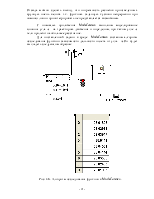
Для поставленной задачи в среде  MathConnex составим алгоритм исследования функции зависимости дальности полета от угла  .Он будет выглядеть следующим образом:

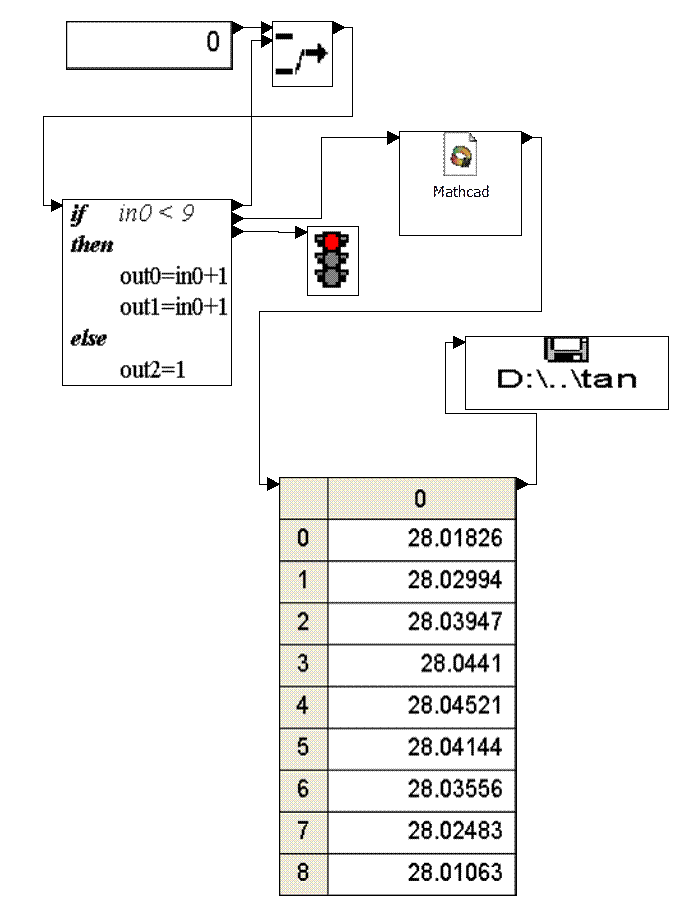
Рис. 3.6. Алгоритм исследования функции в Math Connex.

Содержимое файла MathCAD в MathConnex:

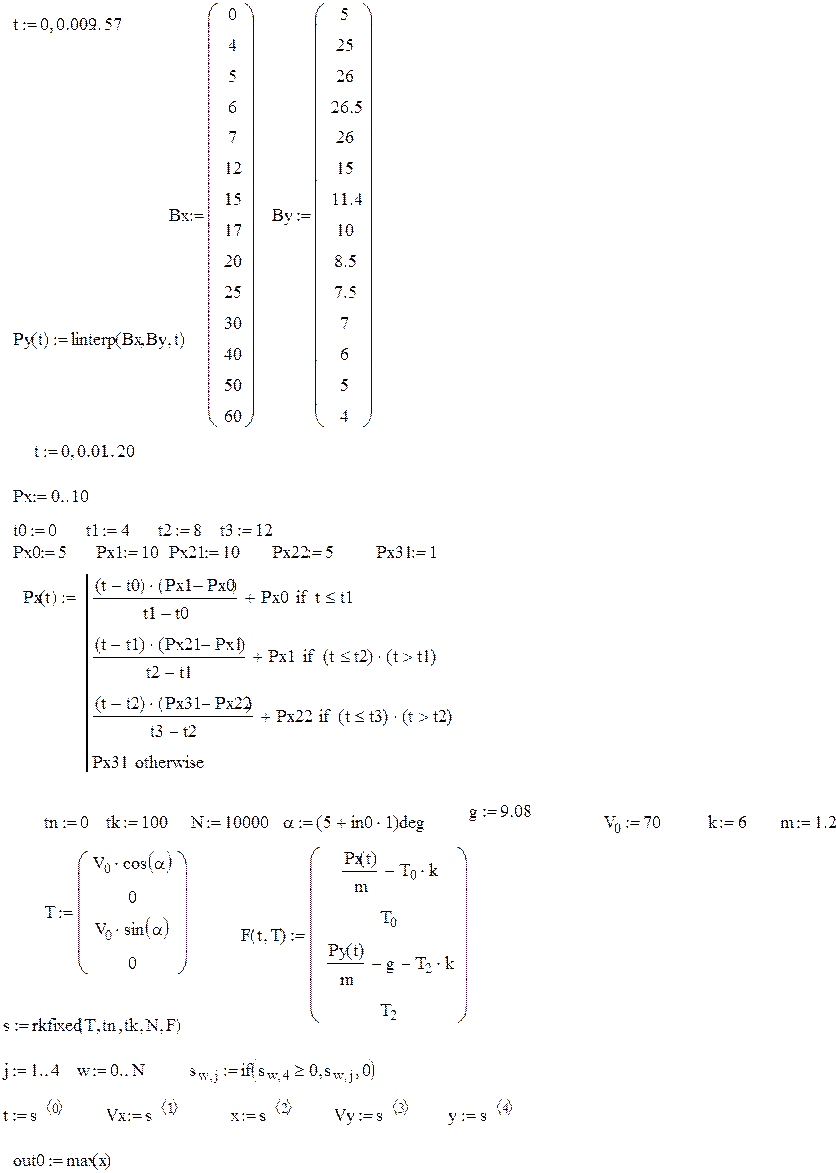
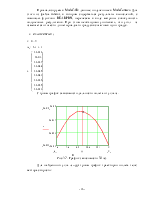
Проанализируем в MathCAD данные, полученные в MathConnex. Для этого из файла tan.txt, в котором содержаться результаты вычислений, с помощью функции READPRN, перенесем в виде матрицы совокупность