формирующейся контактной поверхности с одновременным снятием температурных кривых. Из приведенных исследований пришли к выводу, что даже в жидком состоянии нет «чистого контакта» и даже в твердом нет «чистого зазора». Наблюдения за контактной поверхностью показали, что «отход» отливки от формы происходит случайными пятнами, в основном при затвердевании и этот процесс носит ярко выраженный дискретный характер.
Один из способов решения уравнения нестационарной теплопроводности (1) с граничными условиями - минимизация соответствующего функционала на множестве функций, удовлетворяющих граничным условиям задачи. В рамках вариационного подхода, решение задачи теплопроводности эквивалентно нахождению минимума этого функционала, не имеющего очевидной физической интерпретации. Проводя минимизацию и используя свойства интерполяционного (аппроксимирующая функция в пределах конечного элемента), можно для каждого конечного элемента записать следующее уравнение [7]:
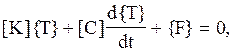 (5)
(5)
где [K] - матрица жесткости (теплопроводности); [С] - матрица теплоемкости; {F} - вектор-столбец тепловой нагрузки; {T} - вектор-столбец искомой функции (функции температуры).
Матрицы в уравнении (5) содержат поверхностные и объемные интегралы. Результаты интегрирования будут зависеть от вида элемента и соответствующего ему интерполяционного полинома. В трехмерной постановке наиболее простым будет решение задачи для случая тетраэдальных элементов с четырьмя узлами. В этом случае аппроксимирующей функцией является линейный полином.
Считая теплопроводность Kn изотропной, можно получить следующие выражения локальных матриц, относящиеся к одному конечному элементу [7]:
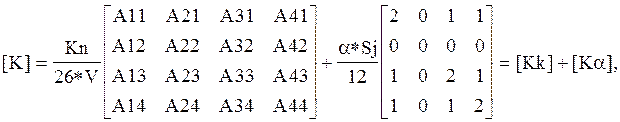
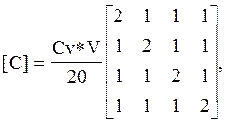 (6)
(6)
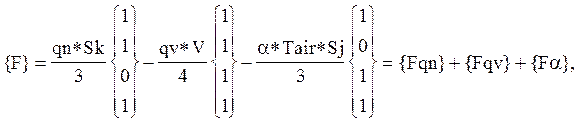
где Aij - коэффициенты, вычисляемые при известных координатах узлов i,j через соответствующие определители [13]; Sj,Sk - площади теплоотводящих граней напротив узлов с индексами j и k соответственно, которым соответствуют нулевые члены в строках и столбцах матриц и вектор-столбцов; [Kk],[Ka] - кондукционная и конвекционная составляющие матрицы теплопроводности соответственно; {Fqn},{Fqv},{Fa} - поверхностная, объемная и конвекционная составляющие тепловой нагрузки соответственно.
Теплоемкость, теплопроводность и другие исходные теплофизические характеристики для каждого конечного элемента вычисляются в зависимости от начальной температуры его узлов и могут меняться на каждом расчетном шаге по времени.
Суммируя узловые значения матриц (6) поэлементно, получим уравнение глобальных матриц аналогичное (5), но относящееся уже не к отдельному
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.