





















функций для численного решения дифференциального, в результате действия которых получается матрица, содержащая значения функции на некотором интервале значений аргумента, например при решении дифференциального 1-го порядка получим матрицу из двух столбцов, где 1-ый столбец показывает значения аргумента в заданном диапазоне, а 2-ой столбец искомые значения функции.
![]()
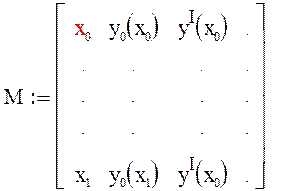
каждая из встроенных функций требует следующего:
1. Задание диапазона изменения независимой переменной (задание точек, в которых нужно найти решения).
2. Задание начальных условий и записанная в специальном виде диф. уравнения.
Функция Рунге-Кутта
rkfixed(y,x0,x1,k,D)
ü y – вектор начальных условий, размерности n (для уравнения 1-го порядка вектор превращается в одну точку).
ü ![]() ,
, ![]() - граничные точки на котором ищутся
решения дифференциального уравнения.
- граничные точки на котором ищутся
решения дифференциального уравнения.
ü k – количество точек не считая начальной.
ü D – функция с аргументами D(x,y), возвращающая значения в виде вектора из n элементов содержащих первые производные функции.
3.2. Техническое обеспечение.
Для реализации решения поставленной задачи о колебании жидкости в сообщающихся резервуарах с переменным сечением требуется установить систему MathCAD 7 на ПК класса Pentium/Pentium MMX/ Pentium Pro/ Pentium II и выше с ёмкостью ОЗУ не менее 12 Мбайт (рекомендуется 16 Мбайт и выше). На ПК должна быть установлена операционная система Windows 95/98 или Windows NT 3.51 (и выше). Инсталляция в минимальном объеме требует 18Мбайт на жестком диске, а в типовом 55 Мбайт. Документ с решением занимает 33.2 кбайт на жестком диске. Для получения листинга необходим принтер.
4. Исходные данные.
Для решения задачи требуется знать следующие величины:
1) ![]() – начальные значения угла поворота
кривошипа, они равны соответственно 35, 27, 15 градусов.
– начальные значения угла поворота
кривошипа, они равны соответственно 35, 27, 15 градусов.
2) ![]() – начальные
значения перемещения ползуна, они равны соответственно 1.1, 1.2, 0.1 метров.
– начальные
значения перемещения ползуна, они равны соответственно 1.1, 1.2, 0.1 метров.
3) ![]() – длина
звена механизма, равная 0.1 метра.
– длина
звена механизма, равная 0.1 метра.
4) ![]() – угол
между звеньями механизма, равный 125 градусов.
– угол
между звеньями механизма, равный 125 градусов.
5. Описание функционирования.
5.1.Графическая схема алгоритма.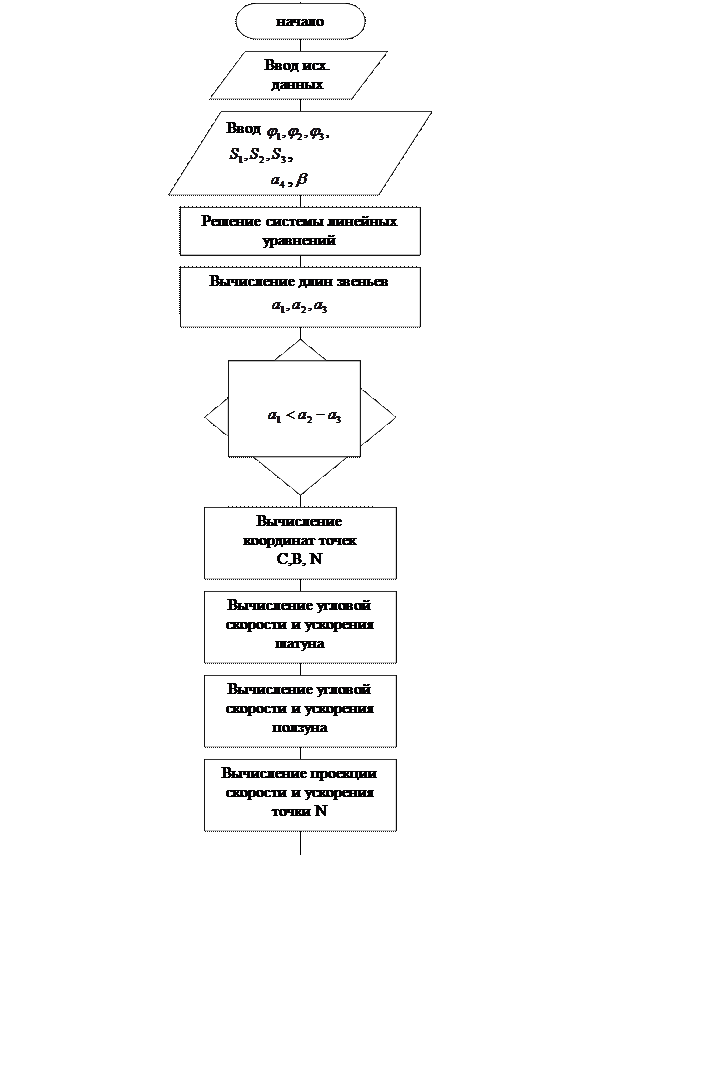
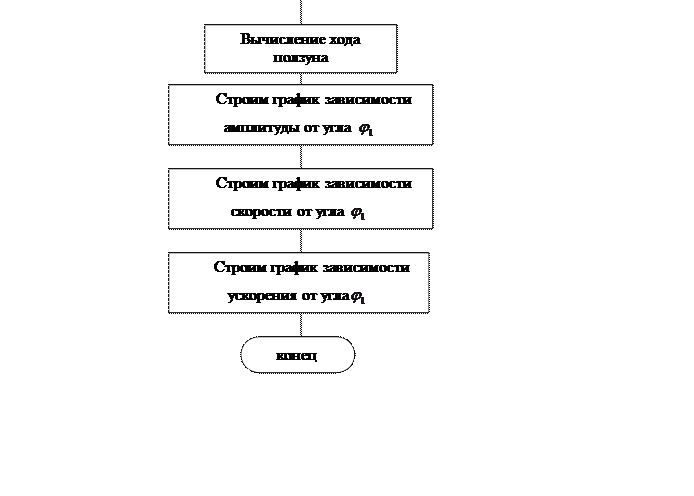
Рисунок 2 – Графическая схема алгоритма
6. Результаты и их анализ.
В результате исследования математической модели передаточного механизма были получены значения перемещения, скорости, ускорения движения точек и звеньев механизма в определенный момент времени в зависимости т угла поворота кривошипа. Были найдены значения длин звеньев, а также проверили условие существования механизма.
Заключение.
В данном курсовом проекте была решена задача о колебательном движении жидкости в сообщающихся резервуарах с переменным сечением. Данная задача решена достаточно полно: был проведён расчет перемещения, скорости и ускорения движения уровня жидкости; построены графики зависимостей перемещения, скорости и ускорения движения уровня жидкости от времени. Также было проведено исследование влияния площадей сечения на время затухания колебаний.
Достоинство программного комплекса в том, что он является хорошим помощником инженеру в исследовании колебательного движения жидкости в сообщающихся резервуарах с переменным сечением. С его можно достаточно точно определить амплитуду, скорость и ускорение в интересующий момент времени.
Недостаток программы в том, что она является узконаправленной, используется в узком диапазоне значений и в ней не предусмотрена защита от неправильного ввода исходных данных.
Литература.
Для создания курсового проекта использовалась литература:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.