Встановлення закону зміни випадкових величин за результатами досліджень, страница 3

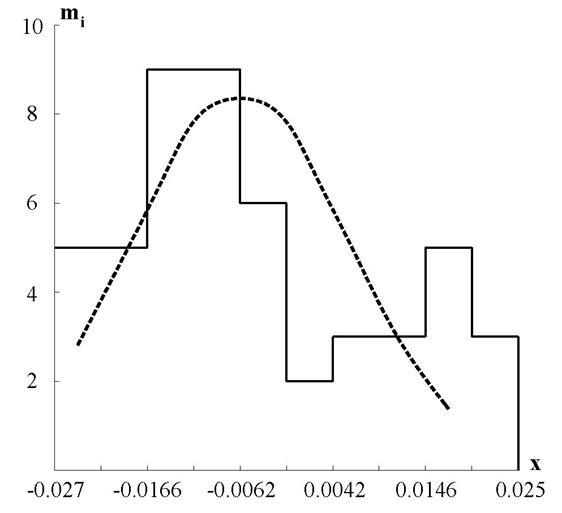
Рис. 3. Графік з врахуванням вирівнювання емпіричного розподілу.

Порівняємо емпіричну та теоретичну функції розподілу частот, використовуючи критерій узгодженості Пірсона.

Критерій Пірсона вигідно використовувати при великій кількості спостережень і у випадку, коли теоретичні значення параметрів функції розподілення невідомі.

Побудуємо таблицю.

Таблиця 5

Номер інтервала (№)				2
1	5	2,81	2,19	4,7961	1,707
2	5	4,82	0,18	0,0324	0,0067
3	9	6,9	2,1	4,41	0,639
4	9	8,25	0,75	0,5625	0,068
5	6	8,25	2,25	5,0625	0,614
6	2	6,9	4,9	24,01	3,48
7	3	4,82	1,82	3,3124	0,687
8	3	2,81	0,19	0,0361	0,013
9	5	1,375	3,625	13,14	9,56

     

   

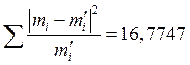
З таблиці знаходимо, що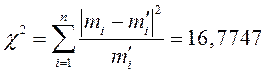

Визначаємо число ступеня вільності:

, де n – число порівнюємих частот, r – число параметрів теор. ф-ції розподілу

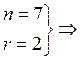 k=4

Використовуючи додаток 2, знаходимо

Криві не узгоджуються.

Порівняємо емпіричну та теоретичну функції розподілу частот, використовуючи теорію Колмогорова.

Найкраще даний підхід використовувати, якщо відомі теоретичні значення параметрів. В інших випадках цей критерій дає дещо завищені оцінки.

Побудуємо таблицю

Таблиця 6

Номер інтервала (№)			(накопичені)	( накопичені)	( накопичені) - ( накопичені)
1	5	2,81	5	2,81	2,19
2	5	4,82	10	7,63	2,37
3	9	6,9	19	14,53	4,47
4	9	8,25	28	22,78	5,2
5	6	8,25	34	31,03	2,97
6	2	6,9	36	37,93	-1,93
7	3	4,82	39	42,75	-3,95
8	3	2,81	42	45,56	-3,56
9	5	1,375	47	46,935	0,065

В колонках 4 і 5 табл.5 представлено накопичені суми, які утворюються шляхом додавання наступних частот до суми попередніх. Потім підраховується різниця між накопиченими теоретичними і накопиченими емпіричними сумами і знаходиться максимальне значення цієї різниці.

Бачимо, що

Тоді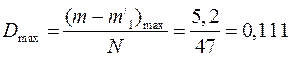

Коефіцієнт Колмогорова

Використовуючи додаток 3, знаходимо . Криві більш-менш узгоджуються.

Висновки

1.  При побудові полігона отриманий провал в центрі. Це вказує на погане налаштування обладнання;

2.  Максимум полігона дещо зміщений, що свідчить про неточне встановлення інструмента;

3.  Графік має різні кути нахилу, що свідчить про вплив на процес обробки стружки, температури, термічних зон;

4.  Діаграма має декілька максимумів, що говорить про використання різних партій деталей;

5.  При аналізі розподілення випадкової величини по критеріям Пірсона і Колмогорова ми отримаємо дещо різні результати. За критерієм Пірсона маємо суттєве відхилення від нормальності розподілення. За критерієм Колмогорова отримуємо більш-менш нормальний розподіл ().

Пропозиції

1.  Потрібно змістити максимум графіка, що можливо при більш точному встановленні інструмента;

2.  Необхідно мінімізувати вплив продуктів оброблення та побічних ефектів на обробку деталей;

3.  Потрібно використовувати деталі однієї партії, що дасть менший спектр відхилення.