|
№ |
Інтервали |
|
Нова випад. велич
|
|
|
|
|
|
|
Більше |
До |
|||||||
|
1 2 3 4 5 6 7 8 9 10 |
-0,027 -0,0218 -0,0166 -0,0114 -0,0062 -0,001 0,0042 0,0094 0,0146 0,0198 |
-0,0218 -0,0166 -0,0114 -0,0062 -0,001 0,0042 0,0094 0,0146 0,0198 0,025 |
5 5 9 9 6 2 3 3 5 3 |
-4 -3 -2 -1 0 1 2 3 4 - |
-20 -15 -18 -9 0 2 6 9 20 - |
80 45 36 9 0 2 12 27 80 - |
-320 -135 -72 -9 0 2 24 81 320 - |
1280 405 144 9 0 2 48 243 1280 - |
|
|
50 |
-25 |
291 |
-109 |
3411 |
|||
Використовуючи формули для об’єма вибірки N>25, обраховуємо наступні параметри:
٠початкові моменти
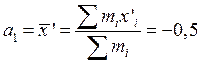
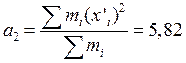
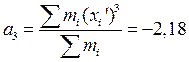
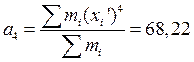
٠центральні моменти
![]() ;
;
![]()
![]()
٠середнє значення та середньо квадратичне відхилення величини х
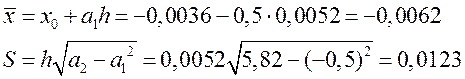
٠показники ассиметрії та ексцесу(кривизни)
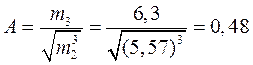
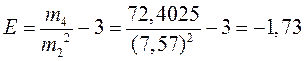
Подальшим етапом розрахунку буде визначення поля допуску. Введемо наступні величини:
![]() вірогідність браку
вірогідність браку
Знайдемо
таке значення ![]() , щоб з наперед заданою
вірогідністю(P
, щоб з наперед заданою
вірогідністю(P![]() ),
), ![]() містив
не менше (1 - 2b) 100% всієї нормальної генеральної сукупності,
містив
не менше (1 - 2b) 100% всієї нормальної генеральної сукупності, ![]() - емпіричне середнє та середньо
квадратичне відхилення відповідно.
- емпіричне середнє та середньо
квадратичне відхилення відповідно.
Покладемо, що ![]() та задаємося вірогідністю
та задаємося вірогідністю ![]() .
.
Використовуючи
таблицю значень l для визначення гарантованого поля допуску, знаходимо,
що для ![]() (
(![]() )
) ![]()
![]() .
.
В такому випадку границі поля допуска:
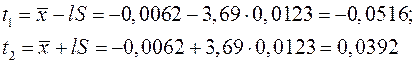
Координати середини поля допуска і половини поля допуска:
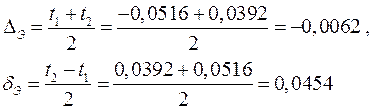
Таким чином, якщо за поле допуска вибрати t2 - t1 = 0,0908, то з ймовірністю 0,9 зі всіх майбутніх спостережень 99,73% буде лежати в цьому інтервалі.
Визначаємо коефіцієнти відносної асиметрії і відносного розсіювання:
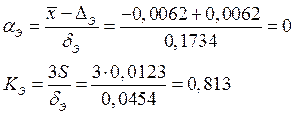
Дивлячись на отримані дані та гістограму, можемо заключити, що:
٠той факт, що гістограма зміщена в напрямку від’ємних значень свідчить про погрішність встановлення інструменту;
٠діаграма містить декілька точок максимума, а, отже, використовувалися різні партії деталей.
Перевіримо, чи вважати випадковим значення (-0,027). Обраховуємо нове середнє значення(без врахування перевіряємого) і середнє квадратичне:
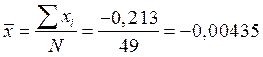
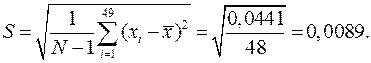
Використовуючи таблицю 8(методичка), знаходимо, що для N = 49 і, наприклад, b = 0,01 значення tb' = 2,713.
Обраховуємо ![]()
Вычисляем ![]() .
.
Отже,
![]() , то з ймовірністю
, то з ймовірністю ![]() значення
(-0,027) можна вважати випадковим.
значення
(-0,027) можна вважати випадковим.
Тепер перевіряємо значення (0,025), використовуючи критерій Ірвіна.
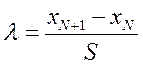
де хN і xN+1 - два найбільших значення випадкової величини.
В данному випадку: ![]() .
.
Тоді:
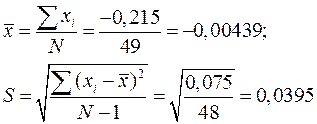
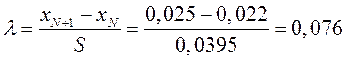
За табл. 9 знаходимо,
що для N = 50 ![]()
![]() . Тому
значення xN+1=0,025 необхідно залишити.
. Тому
значення xN+1=0,025 необхідно залишити.
Проведемо процедуру вирівнювання емпіричного розподілу по гіпотетичним теоретичним.
Даний
закон двухпараметричний. Визначимо попередньо середнє значення ![]() і середнє квадратичне
відхилення
і середнє квадратичне
відхилення ![]() .
.
З табл. 2: ![]() ;
; ![]() .
.
Підставляємо
ці значення у функцію густини, замінюючи ![]() на
на ![]() і
і ![]() на
на ![]() .
.
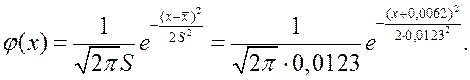
Результати вирівнювання приведені в таблиці 4.
Таблиця 4
|
Номер інтервала № |
Середина інтервала xi |
Емпірич. частоти mi |
|
|
|
Ймовірність інтервалів
|
Теоретич. частоти mi |
|
1 2 3 4 5 6 7 8 9 |
-0,0244 -0,0192 -0,014 -0,0088 -0,0036 0,0016 0,0068 0,012 0,0172 |
5 5 9 9 6 2 3 3 5 |
-0,0182 -0,013 -0,0078 -0,0026 0,0026 0,0078 0,013 0,0182 0,0234 |
-1,48 -1,057 -0,634 -0,211 0,211 0,634 1,057 1,48 1,902 |
0,133 0,228 0,326 0,39 0,39 0,326 0,228 0,133 0,065 |
0,0562 0,0964 0,138 0,165 0,165 0,138 0,0964 0,0562 0,0275 |
2,81 4,82 6,9 8,25 8,25 6,9 4,82 2,81 1,375 |
При підрахунках даних таблиці використовувалися наступні формули:
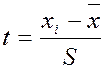
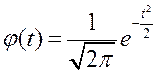
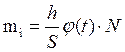
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.