Проектирование цилиндрического одноступенчатого редуктора, страница 4

4.5. Проектный расчет тихоходной степени редуктора

4.5.1 Проектный расчет первой (тихідного) степени редуктора

1. Определяем ориентировочное значение межосевого расстояния

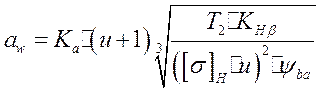
где  Ка- вспомогательный коэффициент Ка=430 мПа;

Т2 - номинальный крутний момент на колесе;

u - предыдущее значение передаточного числа;

- предыдущее значение коэффициента ширины венца зубчатого относительно межосевого расстояния.

 - коэффициент неравномерности нагрузки по ширине зуб венцов ⁼1,07.

=0,4;         u=1,9;               Т2 =242(Нм);

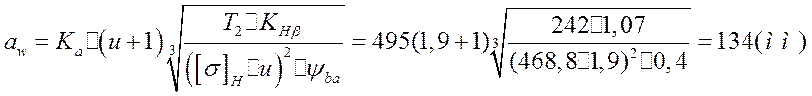
Полученное значение округляем к ближайшему стандартному значению.

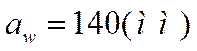
2. Определяем модуль зубчатой передачи

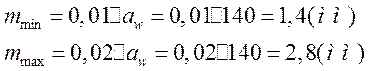
Согласно ГОСТ 9563-60 принимаем      тп= 1,5      мм;

3.Определяем ширину зубчатого венца колеса и шестірні

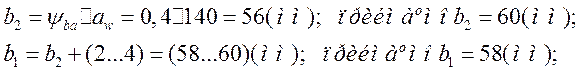
4.Визначаємо суммарное число Z зубцов шестірні и колеса:

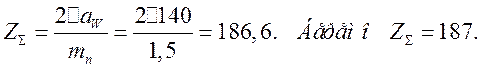
5.  Определяем с число Z зубцов  шестерни:

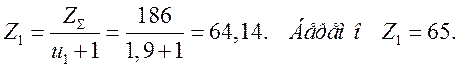
6.  Определяем с число Z зубцов  шестерни:

7.                 Уточняем передаточное число

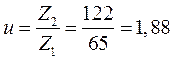
Разногласие с предыдущим значением:

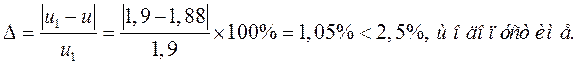
8.  Определяем (для контроля) межосевое расстояние

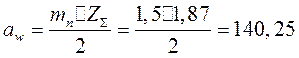
Полученное значение  равняется раньше принятому:

.

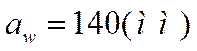1.  Определяем диаметры делительных кругов шестірні и колеса:

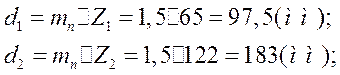
2.  Определяем колову скорость зубчатых колес:

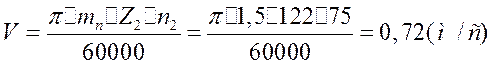
При данной коловій скорости назначаем 9йстепень точности передачи.

4.6. Проверяющий расчет на контактную выносливость.

Расчетное контактное напряжение:

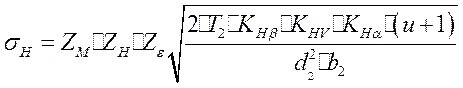
Определяем:

1). Zm- коэффициент, который учитывает механические свойства материалов. Для стальных зубчатых колес Zm=190мПа;

2). ZH - коэффициент, который учитывает форму спрягающих поверхностей зубцов в                                                                                  полюсе зацепления. ZH =2,495;

Коэффициент, который учитывает суммарную длину контактных линий:

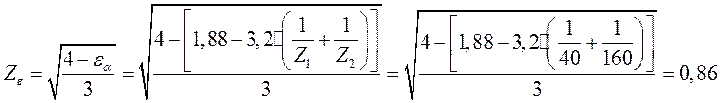
Фактический коэффициент ширины колеса за начальным диаметром: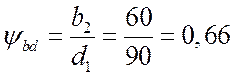

Поскольку то окончательно берем . За табл.З.7

в зависимости от степени точности передачи, твердости поверхности зубцов

Н1,2 < 350 Нв1,2  при коловій скорости V = 1.88 м/с методом інтерполяї

находим коэффициент, который учитывает динамическую нагрузку: Кнv= 1,11. При табл. 3.8 в зависимости от степени точности передачи и колової скорости

V = 1.88 м/с методом интерполяции находим   коэффициент,    что    врахов;

распределение        нагрузки  между  зубцами:   Кна ⁼   1,12.   Поскольку   круг скорость V = 1.54 м/с < 5 м/с то Zv= 1.

Определяем   расчетное   контакте напряжения и проверяем условие:

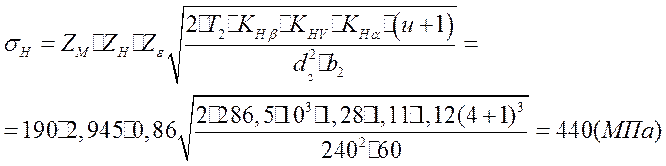
Оцениваем недогрузку:

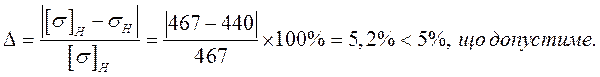
4.7.       Проверяющий расчет на предупреждение пластических деформаций или хрупкого разрушения рабочих поверхностей зубцов от действия

максимальной нагрузки

4.8.      Перевирник расчет на выносливость на изгиб.

Определяем расчетные напряжения изгиба в зубцах шестірні и колеса

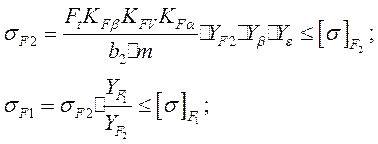
1.  Определяем колову силу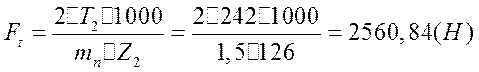

1.  За графиком (рис.3.4, кривая 5) при Н1 < 350НВ1 Н2 < 350НВ2 определяем коэффициент, который учитывает неравномерность распределения нагрузки по длине контактных линий: KFЯ= 1.4

2.   При таблах. 3.9 для 9го степени точности при твердости поверхностей зубцов    Н2< 350НВ1,2 и скорости V = 1.12 м/с определяем коэффициент динамической нагрузки: kfv = 1.06

4. За формулой (3.33)[2] определяем коэффициент распределения нагрузки между зубцами передачи

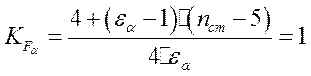
3.  За графиком (рис.3.5) для некорректируемых колес (х2,1 = 0) в зависимости от  Z определяем коэффициенты формы зуба: YF3 = 3,62; YF2 = 3.6

4.  Коэффициент YЯ =1, что учитывает перекрытие зубцов, определяем за формулой

5.  Выполняем проверяющий расчет:

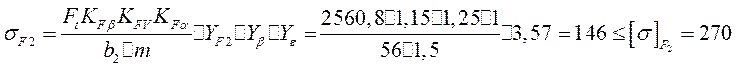
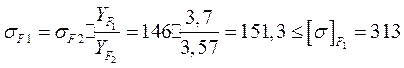
Вывод

Прочность на выносливость при изгибе обеспечена со значительным запасом. Для данной пары зубчатых колес основным критерием работоспособности является контакт прочность, а не прочность на изгиб.