Санкт-Петербургский государственный морской технический университет
Кафедра компьютерной графики и информационного обеспечения
Домашнее задание №2
ЗАДАНИЕ. Построить проекции равнобедренного прямоугольного треугольника АВС (катет равен 200 мм), если АМ и АN направление катетов.
Индивидуальные задания представлены в таблице 1.
Таблица 1
|
Вариант |
Точка А |
||
|
Х |
Y |
Z |
|
|
1 |
300 |
300 |
300 |
|
2 |
350 |
350 |
350 |
|
3 |
400 |
400 |
400 |
|
4 |
450 |
450 |
450 |
|
5 |
300 |
300 |
300 |
|
6 |
350 |
350 |
350 |
|
7 |
400 |
400 |
400 |
|
8 |
450 |
450 |
450 |
|
9 |
300 |
300 |
300 |
|
Вариант |
Точка М |
||
|
1 |
500 |
500 |
300 |
|
2 |
550 |
150 |
350 |
|
3 |
600 |
600 |
400 |
|
4 |
650 |
250 |
450 |
|
5 |
100 |
500 |
300 |
|
6 |
150 |
150 |
350 |
|
7 |
200 |
600 |
400 |
|
8 |
250 |
250 |
450 |
|
9 |
100 |
300 |
500 |
|
Вариант |
Точка N |
||
|
Х |
Y |
Z |
|
|
1 |
100 |
- |
100 |
|
2 |
150 |
- |
150 |
|
3 |
200 |
- |
600 |
|
4 |
250 |
- |
650 |
|
5 |
500 |
- |
100 |
|
6 |
550 |
- |
150 |
|
7 |
600 |
- |
600 |
|
8 |
850 |
- |
650 |
|
9 |
500 |
100 |
- |
|
Вариант |
Точка А |
||
|
Х |
Y |
Z |
|
|
10 |
350 |
350 |
350 |
|
11 |
400 |
400 |
400 |
|
12 |
450 |
450 |
450 |
|
13 |
300 |
300 |
300 |
|
14 |
350 |
350 |
350 |
|
15 |
400 |
400 |
400 |
|
16 |
450 |
450 |
450 |
|
17 |
500 |
500 |
500 |
|
18 |
600 |
600 |
600 |
|
Вариант |
Точка M |
||
|
10 |
150 |
350 |
150 |
|
11 |
200 |
400 |
600 |
|
12 |
250 |
450 |
250 |
|
13 |
500 |
300 |
500 |
|
14 |
550 |
350 |
150 |
|
15 |
600 |
400 |
600 |
|
16 |
650 |
450 |
250 |
|
17 |
700 |
700 |
500 |
|
18 |
800 |
400 |
600 |
|
Вариант |
Точка N |
||
|
Х |
Y |
Z |
|
|
10 |
550 |
150 |
- |
|
11 |
600 |
600 |
- |
|
12 |
650 |
650 |
- |
|
13 |
100 |
100 |
- |
|
14 |
150 |
150 |
- |
|
15 |
200 |
600 |
- |
|
16 |
250 |
650 |
- |
|
17 |
300 |
- |
300 |
|
18 |
400 |
- |
400 |
ПРИМЕР ВЫПОЛНЕНИЯ ДОМАШНЕГО ЗАДАНИЯ №2. Построить проекции равнобедренного прямоугольного треугольника АВС с вершиной прямого угла В на прямой k и стороной АС на прямой L.
Начальное графическое условие
(обязательно его наличие)
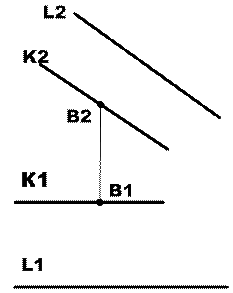
Комментарий к решению задачи: для решения конструктивных задач полезно рисовать модель заданной фигуры в плане, для того, чтобы грамотно использовать ее геометрические характеристики. Одновременно надо внимательно проанализировать начальное условие. На рис.1 представлена модель в плане, а на рис.2 решение поставленной задачи.

Рис.1. Модель задачи в плане.
Из начального условия видно, что заданные прямые kиL параллельны фронтальной плоскости проекций и, следовательно, могут быть сделаны следующие важные выводы (см. рис.2):
- из заданной точки В2 можно проводить линию, перпендикулярную к фронтальным проекциям прямых k2 и L2 одновременно;
-т.к. гипотенуза заданного треугольника должна располагаться на прямой L, то ее фронтальная проекция А2С2 будет равна истинной величине гипотенузы АС.
Сделанные выводы позволяют создать модель решения задачи (рис.1), в которой искомый треугольник построен следующим образом:
- из точки М проведена высота ВМ;
- известно, что высота, проведенная из вершины прямого угла, делит равнобедренный прямоугольный треугольник на два равных равнобедренных прямоугольных треугольника с вершиной прямого угла у основания высоты. Следовательно ВМ=МА, т.е. гипотенуза искомого треугольника в два раза больше его высоты;
- поскольку проекции высоты ВМ могут быть легко построены, то не составляет труда найти истинную величину гипотенузы АС и, следовательно, построить проекции треугольника АВС.
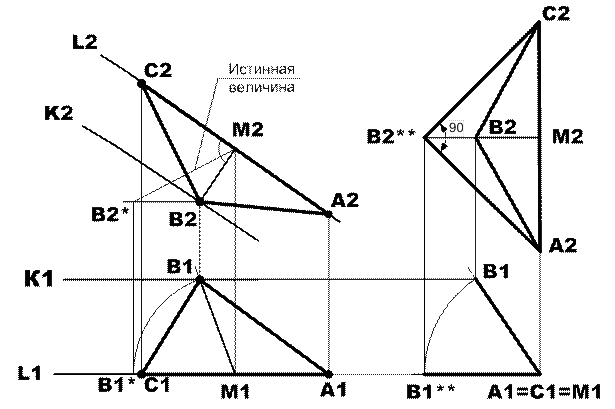
Рис.2. Построение проекций равнобедренного прямоугольного треугольника.
Решение:
1) из точки В2 провести перпендикуляр к L2 и построить проекции высоты В2М2 и В1М1;
2) методом вращения, повернув высоту ВМ до положения параллельного фронтальной плоскости проекций, определить ее истинную величину-это проекция М2В2*;
3) отложить отрезок М2В2* на линии L2 в разные стороны от точки М2 для построения проекций вершин А2 и С2 искомого треугольника;
4) построить фронтальную А2В2С2 и горизонтальную А1В1С1 проекции искомого треугольника.
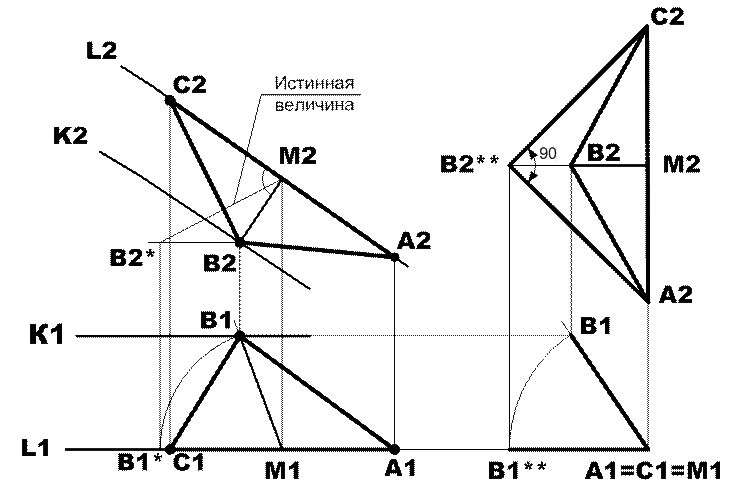
Проверка: построенные проекции треугольника искажены, поскольку заданный треугольник находится в общем положении в пространстве. Убедиться в правильности выполненных построений можно только определив истинную величину треугольника. Для этого методом вращения сначала треугольник переведен в проецирующее положение, которому соответствуют фронтальная проекция А2С2В2 при вертикальном расположении гипотенузы А2С2 и горизонтальная проекция в виде отрезка прямой А1С1В1. Далее проецирующий треугольник надо повернуть до положения параллельного плоскости П2, которому соответствуют горизонтальная проекция А1С1В1** и фронтальная проекция А2С2В2**. При этом проекция А2С2В2** равна по величине истинной. На рис.2 видно, что истинная величина является равнобедренным прямоугольным треугольником с вершиной прямого угла в точке В, что соответствует условию задачи.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.