Пересечение прямой линии и плоскости

Санкт-Петербургский государственный морской технический университет

Кафедра компьютерной графики и информационного обеспечения

ЗАНЯТИЕ 5

ПРАКТИЧЕСКОЕ ЗАДАНИЕ №5

 Пересечение прямой линии и плоскости.

      Если прямая линия пересекает некоторую плоскость, то представляет интерес определение положения точки пересечения прямой и плоскости и при необходимости ее координат.

При графическом решении в общем виде может быть определено положение точки пересечения. Но если необходимо знать координаты точки пересечения, то плоскость и прямая линия должны быть помещены в систему координат. Конечным  результатом определения точки пересечения прямой линии и плоскости в этом случае являются координаты X, Y и Z  точки пересечения.

Плоскости, как правило, являются не прозрачными. Это приводит к тому, что точка пересечения делит прямую на две части – видимую и невидимую (на чертеже показывается пунктирной линией). 

Для того, чтобы найти точку пересечения прямой линии и плоскости, необходимо плоскость перевести в одно из проецирующих положений: перпендикулярно либо к горизонтальной, либо к фронтальной плоскости проекций. В первом случае используется главная линия h, параллельная плоскостиП1, а во втором - главная линияf, параллельная плоскости П2.

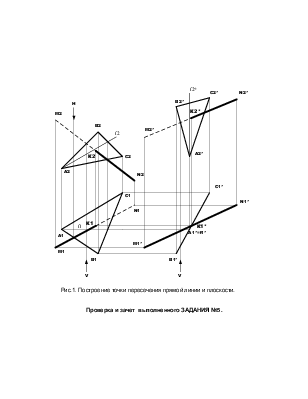
Все построения показаны на рис.1, а их реализация рассмотрена в предыдущем практическом задании.

Определение видимости прямой:

На рис.1 видно, что три проекции линии MN поделены точкой пересечения К на видимый и невидимый участки. Только проекция M1*N1* полностью видна т.к. плоскость проецирующая и, следовательно, не закрывает прямую линию.

Для определения видимости проекций прямой линии используется метод конкурирующих точек.

 Видимость проекции M1N1: конкурирующая точка – точка пересечения  проекций M1N1 и А1В1. Через эту точку необходимо провести вертикальную линию H со стрелкой сверху вниз. Первая встреченная фронтальная проекция (на рис.1 проекция  M2N2) определяет видимую горизонтальную проекцию (на рис.1 проекция M1N1). Поскольку конкурирующая точка находится на отрезке М1К1, то видимым будет только этот отрезок, отрезок же К1N1 будет невидимым.

Видимость проекции M2N2: конкурирующая точка – точка пересечения  проекций M2N2 и А2В2. Через эту точку необходимо провести вертикальную линиюV со стрелкой снизу вверх. Первая встреченная горизонтальная проекция (на рис.1 проекция А1В1) определяет видимую фронтальную проекцию (на рис.1 проекция А2В2). Следовательно, часть проекции М2N2 будет невидимой. Поскольку конкурирующая точка находится на отрезке М2К2, то невидимым будет только этот отрезок, отрезок же К2N2 будет видимым.

Видимость проекции M2*N2*: конкурирующая точка – точка пересечения  проекций M2*N2* и А2*В2*. Все дальнейшие рассуждения соответствуют изложенным выше

 для линии V.

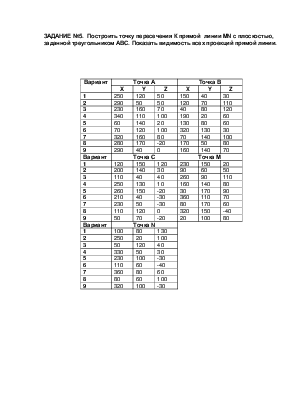
ЗАДАНИЕ №5.  Построить точку пересечения К прямой  линии MN с плоскостью,  заданной треугольником АВС. Показать видимость всех проекций прямой линии.

Вариант	Точка А			Точка В
	Х	Y	Z	X	Y	Z
1	250	120	50	150	40	30
2	290	50	50	120	70	110
3	230	160	70	40	80	120
4	340	110	100	190	20	60
5	60	140	20	130	80	60
6	70	120	100	320	130	30
7	320	160	80	70	140	100
8	280	170	-20	170	50	80
9	290	40	0	160	140	70
Вариант	Точка С			Точка М
1	120	150	120	230	150	20
2	200	140	30	90	60	50
3	110	40	40	260	90	110
4	250	130	10	160	140	80
5	260	150	-20	30	170	90
6	210	40	-30	360	110	70
7	230	50	-30	80	170	60
8	110	120	0	320	150	-40
9	50	70	-20	20	100	80
Вариант	Точка N
1	100	80	130
2	250	20	100
3	50	120	40
4	330	50	30
5	230	100	-30
6	110	60	-40
7	360	80	60
8	80	60	100
9	320	100	-30

                    

                  Рис.1. Построение точки пересечения прямой линии и плоскости.

Проверка и зачет  выполненного ЗАДАНИЯ №5.