Расчет бесстыкового пути на прочность и устойчивость

1. Расчёт бесстыкового пути на прочность и устойчивость.

1.1. Расчётные характеристики подвижного состава.

1.2. Расчётные характеристики пути.

Характеристика	Ед. изм.	Значение
Тип рельса	–	Р65
Приведённый износ	мм	0
Расстояние между осями шпал, lш	см	55
Модуль упругости подрельсового основания, U: лето/зима	кгс/см2	1000/1700
Коэффициент относительной жёсткости подрельсового основания и рельса, , где E = 2,1×106 кг/см2; лето/зима	см-1	13,54·10-3/ 15,46·10-3
Вид шпал	–	ЖБ
Коэффициент, учитывающий отношение необрессоренной массы колеса и участвующей во взаимодействии массы пути, α0	–	0,403
Коэффициент, учитывающий изменения величины колеблющейся массы пути на железобетонных шпалах, по сравнению с путём на деревянных шпалах, α1	–	0,931
Коэффициент, учитывающий влияние типа рельсов на возникновение динамической неровности на пути, β	–	0,87
Коэффициент, учитывающий влияние материала и конструкции шпалы на образование динамической неровности пути, ε	–	0,322
Коэффициент, учитывающий влияние рода балласта на образование динамической неровности пути, γ	–	1
Момент инерции поперечного сечения рельса в вертикальной плоскости, относительно горизонтальной оси, Jв	см4	3540
Момент инерции поперечного сечения рельса в горизонтальной плоскости, относительно вертикальной оси, Jг	см4	564
Момент сопротивления поперечного сечения рельса, относительно наиболее удалённого волокна подошвы, Wп	см3	435
Ширина головки рельса, bг	см	7,5
Ширина подошвы рельса, bп	см	15
Расстояние от нейтральной оси до верха головки рельса, zг	см	9,87
Расстояние от нейтральной оси до низа подошвы рельса, zп	см	8,13
Площадь поперечного сечения рельса, F	см2	82,65
Площадь подкладки, ω	см2	518
Площадь полушпалы с учётом поправки на изгиб, Ωα	см2	3092
Коэффициенты к расчёту напряжений на основной площадке земляного полотна, c1; c2	–	0,245; 0,118
Коэффициент, учитывающий расстояние между шпалами, ширину шпалы и глубину, Ah	–	0,214
Коэффициент, учитывающий неравномерность распределения давления вдоль шпалы и пространственность приложения нагрузки, Η	–	0,7

1.3. Расчёт на прочность элементов верхнего строения бесстыкового пути.

1.3.1. Определение средней вертикальной динамической нагрузки колеса на рельс.

, кг, где               – среднее значение динамической нагрузки колеса на рельс от вертикальных колебаний надрессорного строения экипажа

, кг, где                  – динамическая максимальная нагрузка колеса на рельс от вертикальных колебаний надрессорного строения экипажа

, кг;

, мм.

Подставляем значения переменных в формулы:

 мм;

 кг;

 кг;

 кг.

1.3.2. Определение среднего квадратического отклонения динамической вертикальной нагрузки колеса на рельс.

, кг, где         S_р – среднее квадратическое отклонение динамической нагрузки колеса на рельс от вертикальных колебаний надрессорного строения

, кг;

S_нп – среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс при прохождении колесом изолированной неровности пути

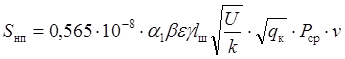, кг;

S_ннк – среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренных масс, возникающих из-за непрерывных неровностей на поверхности катания колёс

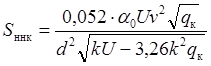, кг;

S_инк – среднее квадратическое отклонение динамической нагрузки колеса на рельс от сил инерции необрессоренной массы, возникающих из-за наличия на поверхности катания колёс плавных изолированных неровностей

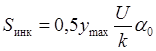, кг, где                y_max – наибольший допустимый прогиб рельса при вынужденных колебаниях катящегося по ровному рельсу колеса с изолированной неровностью

, см.

Подставим значения в формулы:

 см;

 кг;

расчёт S для лета:

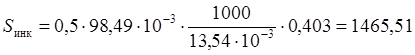 кг;

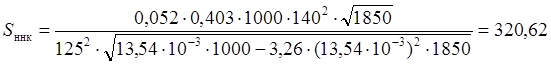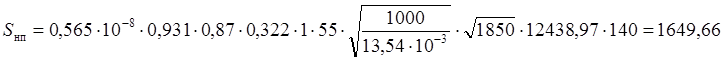 кг;

 кг;

 кг;

расчёт S для зимы:

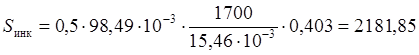 кг;

 кг;

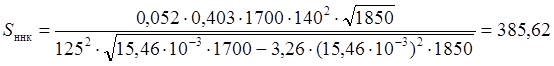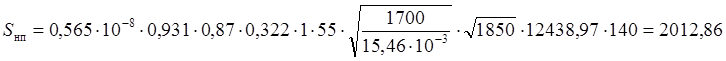 кг;

 кг.

1.3.3. Определение максимальной динамической нагрузки от колеса на рельс.

, где         λ – нормирующий множитель, определяющий вероятность события, т.е. появления максимальной динамической вертикальной нагрузки;