Проект земляного полотна. Определение нагрузки на земляное полотно, страница 2

Данные по этому расчету сведены в таблицу 5 – Р_р и в  таблицу 6 – S_р.

Наличие среднеквадратических отклонений показывают, что все проводимые расчеты являются статистическими. В расчете необходимо показывать возможный диапазон колебаний этих величин. Для наиболее надежной оценки работы пути необходимо учесть максимально возможные силы, которые могут возникать при прохождении подвижного состава по пути. С другой стороны характерно, что для рельсов развитие усталостных процессов наблюдается в местах проявления дефектов (трещин), но так как при значительных усилиях небольшое количество перегрузок не может заметно уменьшить срок службы рельса, поэтому расчет ведется не на максимально возможное значение динамического давления колеса на рельс, а на несколько меньшее – максимальное  с уровнем вероятности непревышения Ф=0,99379.

При расчетах, как правило, не учитываются  силы, возникающие при прохождении изолированной неровности пути, неровности колеса подвижного состава, так как при колебательном процессе эти силы знакопеременны и, как правило, взаимно уничтожаются, учитывая это по правилам расчета, принято учитывать не воздействие самих сил, отклонения, которые они вызывают.

При расчете учитывают:

·  Sp – среднее квадратическое отклонение вертикальных сил, вызываемых колебаниями кузова на рессорах;

·  Sнп – среднее квадратическое отклонение от силы инерции, возникающей при прохождении изолированной неровности пути;

·  Sинк и Sннк – то же, от колес имеющих изолированные и непрерывные неровности на поверхности катания;

Среднеквадратические отклонения определяются по следующим формулам:

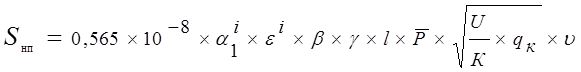
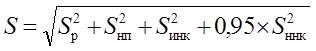
Где:

e - коэффициент, учитывающий влияние жесткости пути на величину уклона динамической неровности( 1 – деревянные шпалы, 0,322 – железобетонные)

b - коэффициент, учитывающий влияние типа рельса на образование динамической неровности на пути (для рельсов Р50,Р65,Р75 соответственно 1, 0,87, 0,82)

g - коэффициент, учитывающий влияние рода балласта на образование динамической неровности на пути.

l – расстояние между осями шпал на эпюре

qк – неподрессоренная масса, отнесенная к одному колесу а1 – расчетная глубина динамической неровности, принимается равной а1=2/3а_1-птэ

d – диаметр колеса

y_max – максимальный дополнительный прогиб рельса при прохождении конусоидальной неровности, определяется по отношению периодов вынужденных колебании системы «колесо – путь»

Расчетные данные для вышеописанных среднеквадратических отклонений приведены в таблицах 7,8,9,10.

После расчета среднеквадратических отклонений производится расчет максимвльно вероятного динамического давления колеса на рельс, по формуле:

Данные о динамическом давлении колеса на рельс приведены в таблице 10а.

1.1.3  Расчет эквивалентной нагрузки.

При расчетах верхнего строения на прочность рельс рассматривается как изогнутая балка на упругом основании. Рельс испытывает давление колес, а в промежутках меду ними на него (рельс) действует только реакция основания – распределенная нагрузка. Расчет ведется по формулам Журавского, прогиб рельса у, изгибающий момент М, давление рельса на шпалу Q определяются по формулам:

На основании этих формул выводят формулы для расчета эквивалентного груза, который заменяет систему сил, будучи приложенным, к расчетному сечению.

Эквивалентный груз рассчитывается по формуле:

В расчете параметр кх зависит от расчетной оси, т.е. той оси, под которой возникает максимальный изгибающий момент. При определении расчетной оси пользуются правилами нахождения расчетных осей для тележек с различным числом осей.

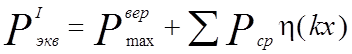
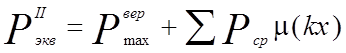
В расчете для данного случая имеем трехосную тележку локомотива ВЛ60 и двухосную тележку вагона. За первую расчетную ось при двухосной тележке принимают первую ось тележки. При трехосной тележки за расчетную принимают первую ось если x=3П/4к < l_min (l_min – минимальное расстояние в тележке между осями колесных пар), вторая ось принимается за расчетную если l_min < x. Расчетные схемы представлены на рисунке 1.