Опорний конспект лекцій з дисципліни "Аналіз електронних схем" (Аналіз електронних схем за постійним струмом. Динамічний аналіз електронних схем), страница 2

Цей вираз називається зворотною формулою Ейлера. Згідно співвідношенню  значення  входить в праву частину (2.5) як аргумент функції . Тому виходять формули, придатні лише для ітераційних розрахунків: по деякому початковому значенню знаходиться при багатократному використанні виразу (2.5). Початкове значення  можна розрахувати за допомогою прямої формули Ейлера (2.4).

Формула трапецій має вигляд

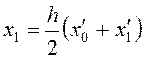                                              (2.6)

2.2 Порядок методу інтеграції і помилка усікання

У формулу трапецій значення похідних в старій і новій точках входять з однаковими вагами. Очевидно, ці похідні можна узяти з різними вагами. Так само можна поступити і із значеннями функцій.

У формулі трапецій шукана функція апроксимована поліномом другого ступеня. Тому говорять, що метод чисельної інтеграції, що спирається на метод трапецій, має порядок р, рівний двом. Погрішність опису функції х(t) поліномом другого ступеня визначається відкинутими членами ряду Тейлора, що містять похідні третього і вищих порядків. У зв'язку з цим перший, не рівний нулю співмножник позначають  і називають помилкою усікання. Для формули трапецій .

Використавши значення коефіцієнтів, для прямої і зворотної формул Ейлера, знайдемо, що порядок інтеграції у цих формул рівний одиниці, а помилка усікання  складає відповідно -1/2 і 1/2. Формула трапецій дає кращі результати, чим дві формули Ейлера. Причина цього в збільшеному порядку інтеграції і меншій помилці усікання. Вище значення р і менша помилка усікання с_р+1 в деякому розумінні краще для результату, що отримується за допомогою формул чисельної інтеграції.

2.3 Усталеність методів інтеграції

Для характеристики методу інтеграції недостатньо знати його порядок і помилку усікання. Важлива ще одна властивість – усталеність методу.

Формула, по якій безпосередньо визначається рішення в наступній точці, подібна до прямої формули Ейлера, називається явною. Явні формули потрібні головним чином для прогнозу початкових значень при використанні інших формул, аналогічних зворотній формулі Ейлера або правилу трапецій, які в основному застосовуються для ітеративного вирішення нелінійних рівнянь алгебри на кожному кроці. Такі формули називаються неявними, або формулами корекції. Об'єднання явних формул з неявними приводить до методу прогнозу і корекції. При цьому розрахунок буде більш трудомістким за рахунок застосування неявних формул. Проте велика усталеність останніх може привести до менших обчислювальних витрат у зв'язку з допустимим збільшенням кроку інтеграції.

Формулу інтеграції називають А-усталеною, якщо вона дає обмежене рішення тестового диференціального рівняння для довільних розмірів кроку і будь-якого числа кроків при . Правило трапецій і зворотна формула Ейлера володіють цією властивістю.

Область абсолютної стійкості даної формули – частина площини , в якій інтеграція диференціального рівняння при  дає обмежений результат для будь-якого числа кроків. Наприклад, пряма формула Ейлера абсолютно стійка усередині кола, що лежить в лівій половині площини. З іншого боку, зворотна формула Ейлера абсолютно усталена у всій лівій напівплощині.

Більшість ланцюгів, що зустрічаються на практиці, є усталеними. Для лінійного ланцюга це означає, що дійсні частини характеристичного коріння негативні. Тому, кажучи про тестове рівняння, мають на увазі рішення при . Проте зустрічаються ситуації, наприклад в автоколивальних системах, коли схема в робочій точці нестійка і в сталому режимі в ній спостерігаються періодичні коливання. При чисельній інтеграції диференціальних рівнянь таких ланцюгів потрібно застосовувати методи, що враховують вказані властивості. Так, зворотна формула Ейлера дає рішення, які затухають з часом, і тому не підходить для подібних завдань. Правило трапецій в таких ситуаціях переважає.

Жорстка система – система, що має декілька полюсів поблизу початки координат і декілька полюсів, вельми віддалених від них, причому всі полюси розташовані в лівій напівплощині. Така система усталена. Компоненти рішення, відповідні далеким полюсам, швидко затухають. Якщо інтегрують, використовуючи пряму формулу Ейлера, то необхідно вибрати розмір кроку h таким малим, щоб значення  для полюса, який найбільш видалений від початку координат, відповідало області стійкості. Вказана умова повинна бути виконана, не дивлячись на те, що компонент рішення, відповідний цьому полюсу, позначається лише на початковій ділянці відгуку. З іншого боку, зворотна формула Ейлера не викликає таких проблем, оскільки вона стійка для будь-яких h. Тому можна почати з малого значення h і потім перейти на більше, як тільки швидкі компоненти затухнуть. Застосування формули, придатної для інтеграції жорстких систем, не вимагає малих розмірів кроку. Проста з них – зворотна формула Ейлера.

2.4 Розрахунок лінійних ланцюгів в тимчасовій області

Формули чисельної інтеграції, про які йшлося в попередніх підрозділах, застосовні для розрахунку як лінійних, так і нелінійних ланцюгів.

Якщо ланцюг описаний рівнянням в нормальній формі відносно змінних стану

                                                                    (2.7)

то часове рішення не викликає проблем.

Рівняння для розрахунку схем в часовій області можна отримати способом, який спирається на так звані супроводжуючі моделі. При такому підході диференціальне рівняння, що зв'язує струм і напругу на конденсаторах або котушках індуктивності апроксимується співвідношенням, яке визначається використовуваним методом інтеграції. У результаті конденсатори і котушки індуктивності замінюються еквівалентною схемою, що містить резистор і джерело струму або напруги. При цьому чисельні значення параметрів еквівалентної схеми залежать від методу інтеграції.

Розглянемо зворотну формулу Ейлера, повторену для n-го кроку

                                            (2.8)

і конденсатор в ланцюзі. Напруга на конденсаторі і струм, що протікає через нього, зв'язані співвідношенням . Позначивши напругу u через х, похідну du/dt = i/c через х', отримаємо

                              (2.9)

Цей вираз може бути переписаний як

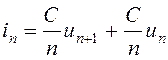                                (2.10)

Величина  є провідністю, а рівняння – супроводжуючу модель конденсатора. Тут ,  – змінні на n-м кроці, тоді як  – джерело струму, сполучене паралельно з . Схожі результати виходять у разі котушки індуктивності, для якої справедливе рівняння . Позначимо струм i через х, а похідну  через х', отримуємо

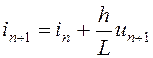                                   (2.11)

або

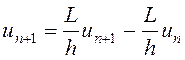                             (2.12)

Цей вираз можна інтерпретувати так: резистивний елемент включений послідовно з джерелом напруги, З вищевикладеного видно, що застосування зворотної формули Ейлера приводить до наступного:

1. Ланцюг стає резистивним. При цьому кожна котушка індуктивності замінюється резистором з опором , а кожен конденсатор - резистором з провідністю .

2. Джерела, що залежать від рішення на попередньому кроці розрахунку, підключаються паралельно резисторам, що мають провідність , і послідовно з резисторами, що мають опор .

Подібні формули можуть бути отримані для правила трапецій або для багатокрокових формул високого порядку. В кожному випадку ланцюг стає резистивним з додатковими джерелами.