Нахождение среднеарифметического значения оценок АКФ для заданных значений задержек

Министерство Образования и Науки Украины

Национальный технический университет

«Харьковский политехнический институт»

Кафедра «Радиоэлектроники»

Расчётно-графическое задание

по курсу:

«Теория вероятностей и математическая статистика»

Выполнил:                                                                                               студент  гр.АП-19а                                            Рудаков  И.А.                                                                        Проверил: Котов Д.В.

Харьков 2010

1.Найдём среднеарифметическое значение оценок АКФ для всех значений

задержек:

                                

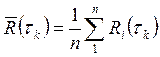                                  n=20,

Где i-номер участка развёртки, n-усредняемое количество участков развертки.

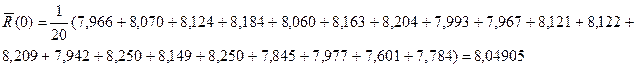
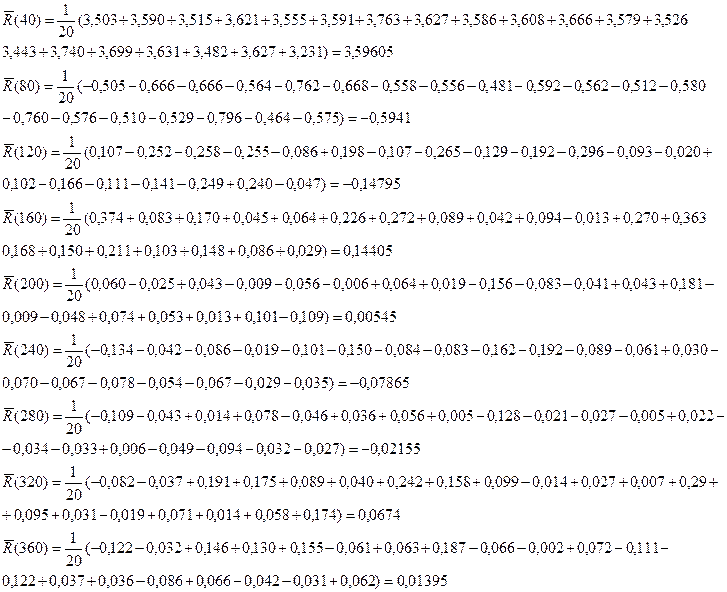
3.Найдём среднеквадратичное отклонение (СКО) для R(0):

-без учёта смещения:

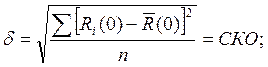                 i=1,2,…20;

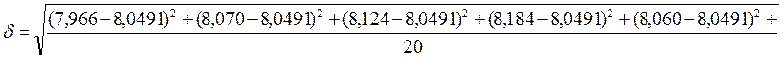
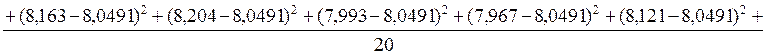
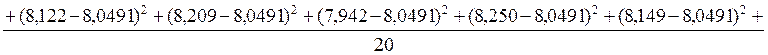
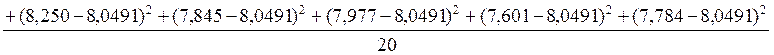=0,204287;

-нормированное (относительное) значение:

                                                  

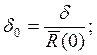
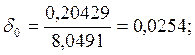
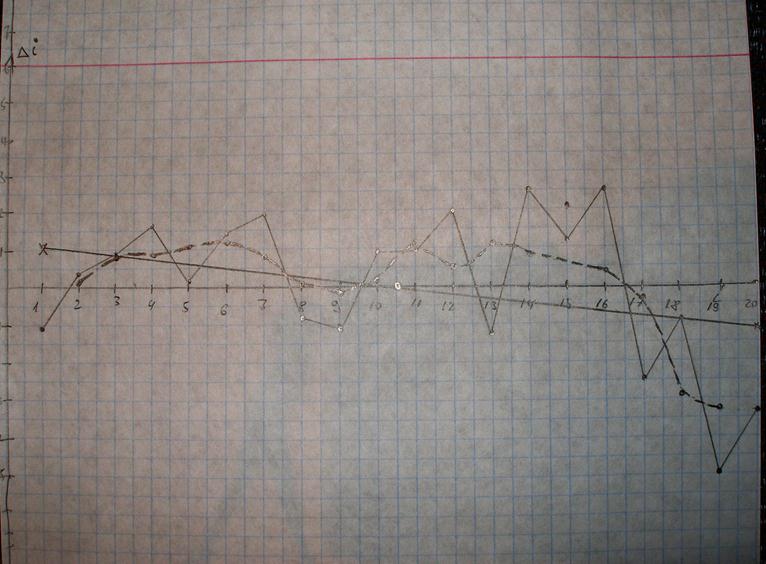
4.Используя отрезки прямых, построим график распределения относительных откло-

нений  (в %) по развёртке дальности:

                                                

                        

                           

                                 

                              

                           

                          

                                                     

                               

                         

                          

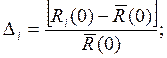
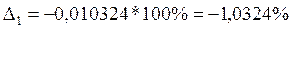
5.Проведём сглаживание по формуле:

                                                                                             

                                     

                                        

                                      

                                                    

                                    

                                     

                                     

                                    

                                  

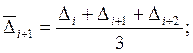
6.Предполагая, что закон изменения функции (i) носит линейный характер, найдём его параметры, используя результаты на основе метода наименьших квадратов для такой зависимости:

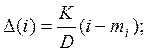                                                    i=1, 2...20;

                                        

                                      

                                       

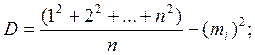
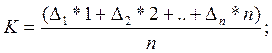
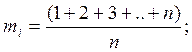
При n=20:        =10,5;         D=33.25;

;

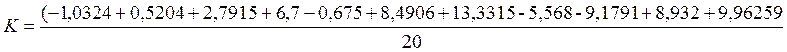
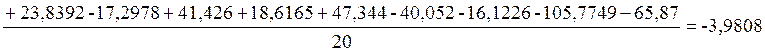Окончательный вид зависимости:

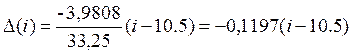                                               i=1, 2...20.

              

7.Предположим, что ошибка измерений имеет случайный характер. Для этого нормируем значения  на :

                                                  

                                                

                                                       

                                                         ;

                                                                                                                                                        

                                                      

                                                       

                                                   

                                                            

                                                     

                                                       

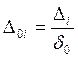
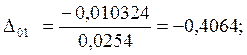
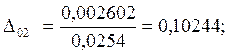
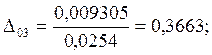
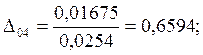
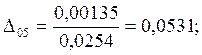
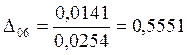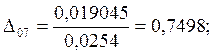
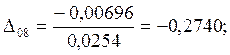
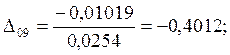
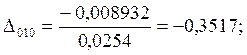
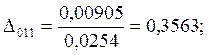
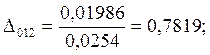
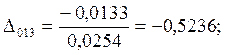
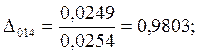
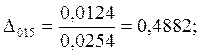
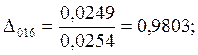
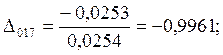
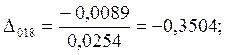
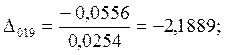
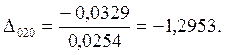
i	19	20	17	13	1	9	10	18	8	5
Δ0i		-1,2953	-0,9961	-0,5236	-0,4064	-0,4012	-0,3517	-0,3504	-0,2740	0,0531

2	11	3	15	6	4	20	12	14	16
0,1024	0,3563	0,3663	0,4882	0,5551	0,4754	0,6594	0,7819	0,9803	0,9803

Для определения закона распределения сведём данные в таблицу:

Разряд	-3; -2	-2;-1	-1;0	0;1	1;2	2;3
Частота	2	3	5	6	2	2
p*	0,1	0,15	0,25	0,3	0,1	0,1
pi равн	1/6	1/6	1/6	1/6	1/6	1/6
pi норм	0,018	0,14	0,34	0,34	0,14	0,018

Используя критерий согласия Пирсона:

                                                  

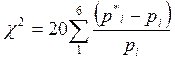
найдём его значение для равномерного закона:

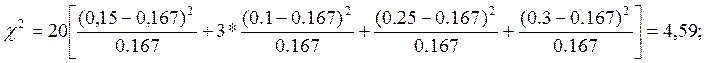
и для нормального:

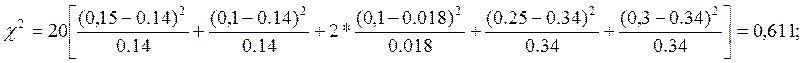
                                                                  p=0.001

Закон распределения не соответствует равномерному закону распределения;

                                                                   P=0.6;

Закон распределения соответствует нормальному закону распределения.

8.Найдём границы доверительного интервала.                                        

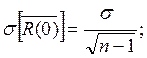                               ,где n=20;

 

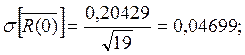
       Вычислим среднеквадратическое отклонение:

Т.к. принято закон распределения считать нормальным, то границы доверительного интервала находим с использованием таблиц, заранее рассчитанных для наиболее употребимых значений доверительных интервалов.

Из заданных таблиц находим оценки границ доверительного интервала:

                                                  При 

                                                 

Границы доверительного интервала: