Определение параметров сигналов и устройств систем передачи информации

Схемы декодера представляет собой схему деления кодовой комбинации V(x) на производящий многочлен g(x). Общий принцип обнаружения и исправления ошибок  при использовании циклического кода заключается в том, что при ошибках деление на приёмной станции идёт с остатком, и если разным ошибкам соответствуют разные остатки , эти последние используются как синдромы. Синдром ошибки может быть теоретическим, а может быть аппаратным. Обычно они не совпадают. Определим теоретические синдромы для одиночной и двойной смежной ошибок, при этом необходимо учесть, что количество импульсов в синдроме должно быть n – k::

1.  Для одиночной ошибки синдром определяется по формуле: x^n-1/g(x).

     Подставим n = 10 и g(x) = x⁴+x³+x²+x+1:

X⁹                                  |x⁴+x³+x²+x+1

X⁹+x⁸+x⁸+x⁷+x⁶+x⁵       x⁵+x⁴+1

X⁸+x⁷+x⁶+x⁵

X⁸+x⁷+x⁶+x⁵+x⁴

X⁴

X⁴+x³+x²+x+1

               X³+x²+x+1

 

Полученный многочлен x³+x²+x+1 отображает синдром для одиночной ошибки.

 

 

 

 

 

 

Но полученный теоретический синдром не отображает своим видом кратность исправляемых ошибок. Докажем, что данный синдром может быть модифицирован, то есть может быть преобразован таким образом, что своим видом будет показывать кратность исправляемой ошибки:

1.  Для одиночной ошибки модификация осуществляется по формуле:

x^n-1*x^n-k/g(x). Тогда получаем:

x¹³                                           |x⁴+x³+x²+x+1

x¹³+x¹²+x¹¹+x¹⁰+x⁹   x⁹+x⁸+x⁴+x³

x¹²+x¹¹+x¹⁰+x⁹

x¹²+x¹¹+x¹⁰+x⁹+x⁸

x⁸

x⁸+x⁷+x⁶+x⁵+x⁴

x⁷+x⁶+x⁵+x⁴

x⁷+x⁶+x⁵+x⁴+x³

x³                                            

 

9. Структурная схема генератора синдромов.

Схема генератора синдромов представляет собой схему деления. Она состоит из техже элементов, что и кодер, причём количество элементов определяется по тем же правилам (см. пункт 3.6.). Построим схему генератора синдромов; она изображена на рисунке 5:

S3

S2

S4

S1

V(x)

2.10. Таблицы состояний элементов регистра сдвига генератора синдромов.

Для описания работы схемы кодера состовляются уравнения функционирования элементов регистра сдвига:

S₁ = D(S₁+S₂+S₃+S₄)           

S₂ = D(S₁)

S₃ = DS₂

S₄ = DS₃

 

	n	e(x)	S1	S2	S3	S4
	1	1	0	0	0	0
	2	0	1	0	0	0
	3	0	1	1	0	0
	4	0	0	1	1	0
	5	0	0	0	1	1
	6	0	0	0	0	1
	7	0	1	0	0	0
	8	0	1	1	0	0
	9	0	0	1	1	0
	10	0	0	0	1	1
	11	0	0	0	0	1

Таким образом  на 11-ом мы получаем аппаратный синдром   Как видно этот синдром соответствует модифицированному теоретически.

Теперь подадим на вход генератора синдромов комбинацию V(x) допустив сначала ошибку во втором такте. Функционирование схемы в этом случаи представлено в таблице 3:

 

Таблица 3

		n	V(x)	S1	S2	S3	S4
		1	1	0	0	0	0
		2	1(0)	1	0	0	0
		3	1	0	1	0	0
		4	0	0	0	1	0
		5	1	1	0	0	1
		6	1	1	1	0	0
		7	0	1	1	1	0
		8	1	1	1	1	1
		9	0	1	1	1	1
		10	1	0	1	1	1
		11	0	0	0	1	1
		12	0	0	0	0	1

Так как ошибка была допущена во втором такте, то синдром появился на n+2 такте (см. табл. 3).  В итоге также получен аппаратный синдром соответствующий модифицированному теоретически.

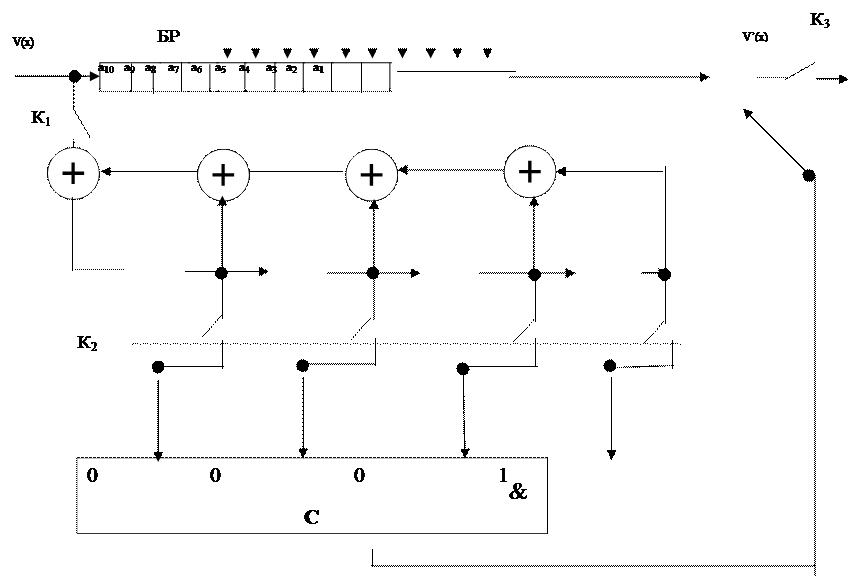
2.11. Структурная схема декодера.

		Рис. 6

 

S2

S3

S4

S1

2.12. Расчёт амплитуды импульсов на входе канала ТУ и длительности импульсов.

Расчитать длительность импульсов Т_и, необходимо найти скорость передачи информации. Это можно  по формуле:

V = 1,1I /Т_пер, где I – количество информации, передаваемой за сеанс связи;

Т_пер – время опроса (мин);

коэффициент 1,1 позволяет учесть длительность    стробирующего импульса.

Тогда Т_и = 1/v = Т_пер/ 1,1I. Подставляя значения из исходных данных, получаем:   

Т_и = 1,2/(1,1*1200) = 0,0009 мин

Теперь найдём общее колличество импульсов N, передаваемое за сеанс связи:

N = Т_пер/Т_и = 1,2/0,0009 = 133,3

Для нахождения Амплитуды импульсов на входе канала ТУ используем следующее выражение:

Р(е) = 0,5(1 – Ф(x)), где Р(е) – вероятность ошибки на выходе канала ТУ;

Ф(х) – функция Крампа, значение которой равно вероятности того, что напряжение помехи превысит некоторое пороговое значение напряжения U_пор.

Согласно исходным данным Р(е) = 3,2*10^-4 , тогда получим:

3,2*10^-4 = 0,5(1 – Ф(х)), следовательно Ф(х) = 1 – 6,4*10^-4 = 0,99936

Аргумент х функции Крампа находится по справочной таблице. В данном случаи х = 3,4. С другой стороны:           

Здесь D – действующее напряжение помехи на выходе канала ТУ.

X=U_п/Ö2*D, => U_п=X*Ö2*D=3,4*Ö2*2,1*10^-3=0,22

U

U

    Напряжение на выходе канала ТУ U_вых = 2U_п = 2*0,22 = 0,44 . Зная затухание канала можно найти U_вх:

Таким образом получаем, что амплитуда импульсов на входе канала ТУ:

 

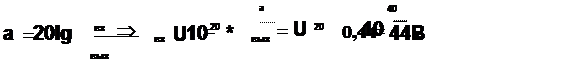А = 44 В

2.13.  Передаточная функция фильтра, согласованного с одиночными импульсами.

огласно исходным данным, информация по каналу ТУ передаётся биимпульсами (см. рис. 7). Передаточная функция фильтра находится по следующему алгоритму:

1.  Найти спектр сигнала, с которым фильтр согласован:

U(jw)₀ò^T(-A*e^{- jwT})dt=-A*/ (-jw)* e^{- jwT}₀÷^T=A/ jw*( e^{- jwT}-1)

2.  Записать комплексно сопряжённый спектр:

U(jw)=A/ jw*( 1-e ^jwT)

3.  Записать передаточную функцию:

H(jw)= U(jw)* e^{- jwT}= A/jw*(1-e ^jwT)*e^{- jw}= A/jw*( e^{- jwT}-1)

Подставив Т = 0,003 мин и А = 37,95 В получим:

 

H(jw)=37,95/jw*( e^{- jwT}-1)

2.14. Схема согласованного фильтра.

    Схему согласованного фильтра строят по передаточной функции H(jw). Полученную в пункте 2.13. передаточная функция может быть представлена в виде трёх сомножителей:

Как известно , умножение на 1/jw в частотной области соответствует интегрированию в пределах от –   до t во временной области а умножение на е^-jwT соответствует задержке сигнала на время Т (е^-jwT = е^-pT = Т – задержка на Т). Следовательно фильтр с функцией передачи вида:

H(jw)=37,95/jw*( e^{- jwT}-1)

состоит из:

                            

- интегратора с коэффициентом передачи 1/jw и коэффициентом