

|
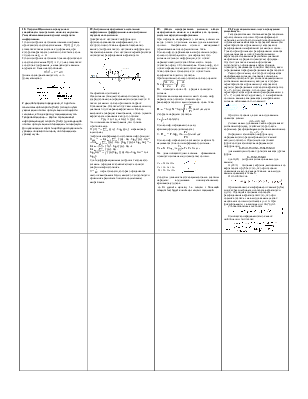
18. Теорема Шеннона о пропускной способности дискретного канала с шумами. Способы повышения верности передачи информации. 1) Если
энтропия источника меньше или равна пропускной способности канала 2)
Если энтропия источника больше пропускной способности канала Длина
последовательности Доказательство:
В данной теореме определено, что достичь максимальной скорости (бит/с) можно путем увеличения полосы пропускания и мощности сигнала и, в то же время, уменьшения шума. Теорема Шеннона — Хартли ограничивает информационную скорость (бит/с) для заданной полосы пропускания и отношения «сигнал/шум». Для увеличения скорости необходимо увеличить уровень полезного сигнала, по отношению к уровню шума. |
19.Энтропия непрерывного источника информации. Дифференциальная энтропия гауссовского сигнала. Дискретному источнику информации противопоставляется непрерывный, т.е. у которого число букв в алфавите бесконечно велико. Энтропия такого источника информации бесконечно велика. Сам источник характеризуется плотностью распределения вероятности.
На практике получается: Все сигналы обладают конечной мощностью, сосредоточенно в определенной полосе частот. К таким сигналам можно применить теорему Котельникова. Отсчеты будут явл. независимыми, значения будут неравновероятными. Можно выполнить операцию квантования, можно оценить вероятность появления каждого отсчета:
Чем меньше шаг квантования, тем точнее приближение.
Энтропия непрерывного источника информации:
Где n-дифференциальная энтропия Гаусовского сигнала, определяет конечную часть полной энергии непр.источника
|
20. Объем непрерывного сигнала, объем непрерывного канала и способы его деления, системы передачи информации. При передаче непрерывного сигнала, сигнал на входе отлич. от сигнала на выходе на величину помехи. Напряжение помехи накладывает ограничение на число различимых букв. Кол-во инф. содержащееся в непр. сигнале опред. кол-вом отсчетов, необх. для передачи этого сигнала и кол-вом информации, кот. может перенести каждый отсчет. Мин. необх. число отсчетов опред. т. Котельникова. Кол-во инф., кот. может перенести каждый отсчет зависит от числа букв отсчетов и точности с кот. может быть воспринят каждый из отсчетов. Приблизительно кол-во отсчетов можно оценить:
Pп – мощность помех Рс – средняя мощность сигнала Отсчеты
явл. независимыми. наиб. кол-во инф. переносимое отсчетом обеспеч. при
равновероятности и взаимонезавис. появ. букв. Скорость передачи отсчетов
Кол-во
инф. передаваемое за ед. времени(производительность) Кол-во инф. переносимое сигналом за время Тс называется объемом непрерывного сигнала.
Dc – динамический диап. cигнала – превышение мощности сигнала над мощностью помехи.
Способы деления:частотное(аналоговые системы передачи: воздышные линии,кабельные), временное,кодовое по Dс делить нельзя, т.к. сигнал с большей мощностью будет влиять на сигнал с меньшей. |
21. Гауссовский канал и его пропускная способность. Гауссовский канал учитывает вероятностные хар-ки сигнала и помехи. При непрерывной передаче самой простой и наиболее применяемой моделью канала является гауссовский канал. Он характеризуется нормальным (гауссовским) распределением напряжений сигналов и помех. Только при нормальном распределении имеется однозначная связь между распределением вероятностей появления различных значений напряжения и средней мощностью процесса. Поэтому для таких каналов пропускная способность, определенная через средние мощности, оказывается точной и такой же, как и определенная через распределения вероятностей. Рассмотрим канал, по которому
передаются непрерывные сигналы. Значения сигналов в моменты отсчетов будем
считать независимыми случайными величинами, каждая из которых характеризуется
нормальным (гауссовским) законом распределения плотности вероятности с σс2=
Рс. Будем считать, что помехи также характеризуются нормальным
распределением с σп2= Рп и действуют
аддитивно, т. е. напряжение помехи в канале складывается с напряжением
сигнала, передаваемого по каналу
При этих условиях, если на входе канала появится сигнал y(t)=si(t)+n(t) Сигнал на выходе канала также представляет случайный процесс, отсчёты которого есть нормально распределённые случайные величины с σу2= Рс+ Рп Определим количество информации, передаваемой по рассматриваемому каналу каждым отсчетом. Воспользуемся общей формулой для количества передаваемой информации R=H(A)-H(A/B)=H(B)-H(B/A) для нашей цели более удобной является другая форма R=H(B)-H(B/A) где Н (В) – энтропия сигналов на выходе канала; Н (В/А) — условная энтропия, вычисляемая по вероятностям р (bj/ai) того, что при условии появления на входе канала буквы ai на выходе канала появляется буква bj. В этой формуле
Применительно к непрерывному каналу р(b/а) следует рассматривать плотность вероятности ω(у/si). Последняя условная плотность распределения вероятностей того, что при посылке отсчета si на выходе канала за счет наложения помехи получается y=si+n. При фиксированном si величина ω(s+n/s)=ω(n). Соответствующая энтропия
Количество передаваемой но каналу информации, бит/отсчет,
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
22. Помехоустойчивые коды. Классификация. Блочные линейные (n, k) – коды, уравнения формирования контрольных элементов, проверки, синдром ошибки.
Блочные n-k коды Совокупность
n=7
k=4 n-k=3 , где k- число информационных симв. Этот код разделимый, потому что четко указаны места информ. и кодовых символов. 2^4 – разрешенные 2^7 – общее число Вес кодовой кобинац (w)– кол-во единиц в ней Кодовое расстояние (d) – кол-во различных разрядов 1101101 – w=5 1011101- w =5, d=2 Ур-я формирования составл. по H (проверочная матрица) a1+a2+a5=a6 11001 | 100 … < 10010 | 010 a2+a3+a4=a8 01110 | 001 Ур-я проверок: переносим an после «=» влево и приравниваем к нулю. По этим ур-ям находим dmin, t=dmin-1 – обнаруж. способн. S=[dmin-1/2]-исправл. способн. Также по ним строится кодер и декодер. Признаком (синдромом) ошибки является совокупность проверок, отличных от нулевой |
23.Геометрическое представление n, k - кодов. Операции над векторами в пространстве кодовых комбинаций , кодовое расстояние, вес кодовой комбинации, минимальное кодовое расстояние. Блочными
линейными n, k кодами
,называется совокупность Кодовое расстояние- это количество символов которыми отличаются две кодовые комбинации. d(Ui; Uj)=Uj-101010 Вес кодовой комбинации- количество единиц; W(Ui)=4 Ui-110101 Мин. кодовое расстояние- минимальный вес кодовой комбинации , находящийся в производящей матрицы кода, т.е. минимальное число единиц в строчке этой матрицы.(dmin) Любую
кодовую комбинацию можно рассматривать как вектор в n-мерном
пространстве.0 и 1 проекции на оси координат. Пусть n=3=>
Эти вектора образуют базис. Из этих трех можно получить остальные путем линейных комбинаций.
Операции с векторами: Сложение, вычитание, скалярное произведение, умножение на число. Скалярное пр-е перпендикулярных векторов=0 |
24. Способы задания линейный (n,k) кодов на примере заданного кода. Задать такой код можно с помощью ур-ий формирования или с помощью ур-ий проверок; также с помощью матриц: проверочной (H) или производящей (G). Ур-е формирования: (n,k) = (7,4) Vi=a1,a2,a3,a4,a5,a6,a7. k= 4 (a1,a2,a3,a4); n-k = 3=( a5,a6,a7) ур-ий столько, сколько контр символов n-k Пример: Ур-я формирований: a1+a2=a5 a1+a3=a6 a1+a3+a4=a7 + - слож по mod2 По ур-ям формир строится схема кодера Ур-я проверок: a1+a2+ a4+a5=0 a1+ a2+a3+a6=0 a1+a3+a4+a7=0 Если справа все нули, то ошибки либо не обнаружены, либо их нет. По ур-ям проверок составляем матрицу H 1101 100 1110 010 1011 001 Если в матрице E – подматрица – систематический код. Транспонируя матрицу, получим производящую G матрицу. 1000 111 2^k =2^4 – разреш код комбин. 0100 110 dmin – наименьшее число едениц 0010 011 в строке = 3. 0001 101 Отсюда: t=3-1=2 – обнаруж способность кода S <= (dmin-1)/2 = 1. – исправляющая способность. |
26. Связь между параметрами кода n и k для исправления ошибок различной кратности. Совершенные , плотноупакованные коды. Производящая матрица кода, исправляющего ошибки первой кратности. Структурная схема кодера кода (7,4). n-кол-во символов сообщения k-кол-во информационных символов n-k – кол-во контрольных символов
Если это неравенство переходит в равенство, то код называется совершенным или плотноупакованным. Например код (7,4):
Примером совершенных кодов явл. коды Хэминга(линейные): (3,1),(7,4),(15,11) и.т.д Чтобы код исправлял ошибки 2-ой кратности нужно, чтобы:
Чтобы код исправлял ошибки 3-eй кратности нужно, чтобы:
Пустьестькод a1 a2 a3 a4 a5 a6 a7 Проверочная матрица Hnx(n-k)
где
В матрице единицами записываются символы участвующие в проверке. Производящая матрица кода Gnxk
Где:
Структурная схема кодера
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
27. Проверочная матрица кода, испр. ошибки первой кратности. Структурная схема декодирующего устройства на примере кода (7,4). Чтобы
код испр. ошибки 1-ой кратности надо, чтобы Если
Строим ур-ния формирования
Ур-ния проверок, исп. для построения декодера.
Сост. проверочную матрицу
единицами запис. символы, участвующие в проверках. Признаком ошибки явл. совокупность результатов проверок отл. от нулевой. Совокупность этих проверок запис в виде столбцов (1ых 4х) в матрице Н.
схема ДКУ |
28. Циклические линейные(n, k) коды. Производящий полином g(x) циклического кода. Его свойства. Признак ошибки в циклических кодах. Линейный n, k код называется циклическим если при циклич.сдвиге вправо(влево) на n-1 разрядов кодовой комбинации, принадл-ие этому коду, образуют комбинации так же принадлежащие этому коду.
Для описания циклич.линейных n, k кодов исп-ся алгебра полиномов от формальной ~ х.
Где
Циклич. n, k код совокупность n, kполиномов, кратных некоторому полиному, называется производящим. Признаком ошибки циклич.n, k кодах является остаток при делении кодовой комбинации на производящий полином.
Чтобы не повышать разряд полагают, что xn=1 xn-1=0; xn+1 – модуль по умножению. Для того чтобы построить некоторый циклический n, k код надо найти такой полином, который обладает наибольшей степенью из всех и все кодовые комбинации делились без остатка. с-ва производящего полинома 1)Степень g(x)=n-k 2n-1-1 ≥ n – исправляет ошибки 1ой кратности 2)
3) g(x)-должен быть неприводимым, его нельзя разложить на множители. g(x)=g1(x)g2(x) – для ош. 2ой кратности. 4) dmin=сумма многочленов в полиноме g(x). Если выполняются эти 4 условия, то код совершенный или плотноупакованный. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
29. Циклические линейные (n, k) коды. Алгоритм кодирования в несистематический код. Условие гарантированного обнаружения ошибки циклическим кодом. Линейный (n,k) код называется циклическим, если при циклическом сдвиге символов кодовой комбинации на один разряд вправо (влево) образуются комбинации, также принадлежащие коду.Циклический n-k код – совокупность кодовых полиномов, кратных некоторому полиному, называемому производящим. Кратность полиномов (деление без остатка ) (n,k) код- С Любая кодовая комб-я Алгоритм кодирования циклических n-k кодов. 1)l – последовательность информационных символов. l(x) – соответствующий ей полином. 2)U(x)=l(x)∙g(x); U(x)→U (n, k) – (7-4);
1) l – 1001 2) U – 1010011
Код гарантир. обнаруж. ошибки, если степень полинома ошибки на единицу меньше производящего полинома. |
30.Структурная схема кодера несистемат линейного n,k –кода на примере кода 7,4.Уравнения функционирования и таблица состояний. Условия правильного построения схемы. Схема составал из 3х d-тригеров и 2х сумматоров g(x)=x3+x+1 Канонич форма записи: g3x3+g2x2+g1x1+g0x0 g2=0 Где g=1 –там цепи сумматоров Нет цепи обратной связи.На вх.канала и декодера комбинац. начинаются со старшего разряда.
D –задержка на 1 такт S1=DL S2=DS1 S3=DS2 V=L+S2+S3
|
31.Алгоритм кодирования в систематический циклический код. .Структурная схема кодера систематического линейного n,k –кода на примере кода 7,4. Уравнения функционирования и таблица состояний.Построение схемы на произвольном производящем полиноме. Алгоритм. 1) l→l(x) 2) l(x)xn-k 3)
4)V(x)=l(x)xn-k+R(x) Пример: 1)l-1001(k) – l(x)=x3+1 2) (x3+1) x3=x6+ x3 3) 4)V(x)= x6 + x3+ x2+x KK: 1001 110
Схема кодера
На выходе 1 кодера всегда ставится сумматор. К=1: S1=D(l+S2+S3) S2=DS1 – задержка на 1 такт S3=DS2 K=2:уравнения состояния написать не удается,поэтому( S2+S3)
|
32.Алгоритм декодирования циклического кода. Генератор синдромов,назначение, структурная схема генератора синдромов на примере кода(7,4).
Алгоритм:
r=n-k – обнаруживает пакеты ошибок pn o <= pek(dmin-1)- если известна вероятность одиночной ошибки Генератор синдромов: g(x)= x3+x+1
ГС выполняет 2 ф-ции: 1.Определяет наличие ошибки в принятой КК путём её деления на производящий полином 2.Формирует универсальный синдром исправления ошибки 1й кратности в любом из разрядов КК кода (7,4) Для его определения на вход схемы подается код Е=1000000 S1=D(E+S1+S3) S2=DS1 S3=DS2
SA-аппаратный синдром ошибки |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
33. Структурная схема декодера систематического линейного n,k –кода на примере кода 7,4.Принцип работы схемы. g(x)=x3+x+1
После 11 такта К3 замыкается и оставшиеся 3 контр символа стираются для систем n,k кода S1=D(V’+S2+S3) а1=1 S2=DS1 а2=0 S3=DS2 а3=1 (ошибка в а3)
SA - аппаратный синдром ош. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.