МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
ИНЖЕНЕРНОЙ ЭКОЛОГИИ
Кафедра “Системы автоматизированного проектирования”
Контрольные задания
ПО ДИСЦИПЛИНЕ “МАШИННАЯ ГРАФИКА И ГЕОМЕТРИЧЕСКОЕ МОДЕЛИРОВАНИЕ”
Составитель Н.И.Гданский
Москва 2001
1. Построение кривых в векторной форме
2.
Написать программы для вычерчивания из произвольного центра следующих параметрических кривых.
1. ![]() ;
; ![]() ,
, ![]() , а=10, b=20.
, а=10, b=20.
2. 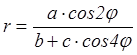 ;
; ![]() a=40;
b=4; c=1.
a=40;
b=4; c=1.
3. 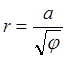 ;
; ![]() a=80.
a=80.
4.r = (a+b sinj) j ; a = 10; b = 5; 0 £ j £ 10p.
5.y = a x 2 + b x + c ; a = 0,05; b = 0,5; c = 30; -50 £ x £ + 50.
6.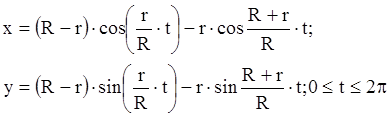
R=40; а) 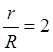 ; б)
; б) 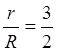 ; в)
; в) 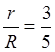 ; г)
; г)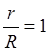 .
.
7.![]() ;a=60.
;a=60.
8. 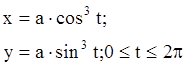 ;
a=100.
;
a=100.
9.![]() ; a=100;b=30.
; a=100;b=30.
10.r = a + bj + cj 2 ; a = 10; b =2; c=0,02; 0 £j£ 6p..
11. ![]() ; a=40.
; a=40.
12. ![]() ; a=50;b=2;c=0,5.
; a=50;b=2;c=0,5.
13. 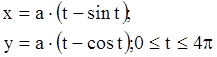 a=20.
a=20.
14. 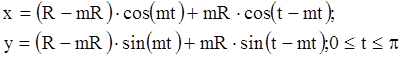
R = 30; m = 0,3.
15. 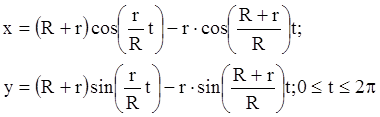
R = 30; r = 15.
16.y = a / (x + b) + c ; a =700; b = -5; c = 10; 10 £ x £ + 250.
17. x = a cosj ;.
y = b sinj ; a =70; b =25; 0 £ x £ + 250; 0 £j£ 6p..
2. Интерполирование и аппроксимация кривых и поверхностей
1. На моделируемую кривую у(х) в узлах х0 , х1 наложены следующие геометрические условия: у(х0) = у0 ; у¢ (х0)=у¢0 ; у(х1) = у1 ; у¢ (х1)=у¢1 . При каком количестве параметров синтеза всегда возможна интерполяция кривой, а при каком – аппроксимация?
2. В узлах х0 , х1 , х 2 на моделируемую кривую, форма которой задана шестью коэффициентами, наложены следующие геометрические условия: у(х0) = у0 ; у¢ (х0)=у¢0 ; у(х1) = у1 ; у¢ (х1)=у¢1 ; у¢¢(х1) = у¢¢1; у(х2) = у2 ; у¢ (х2)=у¢2 . Возможна ли в общем случае интерполяция данной кривой?
3. Найти степень полинома k и матрицу А (по возможности в численном виде) для определения коэффициентов полинома `С =(C0, C1, …,Ck ) для следующих наборов геометрических условий:
а) задача 1 , б) задача 2 , в) n=3; х0 = 0 ; х1 = 1 ; х2 =2 ; х3 =3;
у(х0) = 0 ; у (х1)= 2 ; у(х2) =5 ; у (х3)=6;
г) n=2; х0 = -1 ; х1 = 0 ; х2 =1 ;
у(х0) = -2 ; у¢(х0) = 2; у(х1)= у¢(х1)=1; у(х2) = 1,5; у¢(х2) =0;
д) n=2; х0 = 1 ; х1 =3 ; х2 =4 ;
у(х0)=у¢(х0)=1; у(х1)=2; у¢(х1)=у¢¢(х1)=0; у(х2)=1; у¢(х2)=- 2.
4. Найти выражения для функций Лагранжа и построить полиномы Лагранжа для следующих случаев интерполирования по однократным узлам:
а) задача 1, б) n=2; х0 = 1 ; х1 = 2 ; х2 =3 ;
у(х0) = - 2 ; у (х1)= 1 ; у(х2) = - 4 ;
в) n=3; х0 = -1 ; х1 = 0 ; х2 =1 ; х3 = 2 ;
у(х0) = 10 ; у (х1) = 5 ; у(х2) = - 1 ; у(х3) = 1 .
5. Найти разделённые разности и построить интерполяционные полиномы Ньютона для геометрических условий из задач 4 а), 1 б), 1в).
6. Найти выражения для функций hi (x) и Нi (x) и построить полиномы Эрмита для следующих случаев интерполирования по двукратным узлам:
а) задача 1 б) задача 3.г , в) n=2; х0 = -2 ; х1 = 0 ; х2 =2 ;
у(х0)=-8; у¢(х0)=2 ; у(х1)=1; у¢(х1)=0; у(х2) = -1 ; у¢ (х2) = - 2; г) n=3; х0 = 0 ; х1 = 1 ; х2 =2 ; х3 =4 ;
у(х0) = 10 ; у¢ (х0) = - 1; у(х1) = 6 ; у¢ (х1) =0 ; у(х2) = 1 ;
у¢ (х2) = 2; у(х3) = 4 ; у¢ (х3) = 1.
7. Найти разделённые разности и построить обобщенные интерполяционные многочлена Ньютона для геометрических условий из задач 6 а), 1 б), 1в), г).
8. Найти выражения для функций Лагранжа и построить квадратичные формы для следующих случаев интерполирования поверхностей по однократным узлам:
а) n=1; х0 = 1 ; х1 = 2 ; m =2; y0 = 1 ; y1 = 2 ; y2 =3 ;
z0,0 = 1; z0,1 = 4 ; z0,2 = 5 ; z1,0 = 2 ; z1,1 = 3 ; z1,2 = 6 ;
б) n=2;х0 =-2 ; х1 = -1;х2 = 1; m =2; y0 = 1 ; y1 = 2 ; y2 =3 ;
z0,0 = -10; z0,1 = -6 ; z0,2 = z1,0 = -4 ; z1,1 = -2 ; z1,2 = 0 ; z2,0 = z2,1 = 1 ; z2,2 = 4.
8. Найти выражения для функций hi (x), Нi (x), hj(y), Нj (y) и построить квадратичные формы Эрмита для интерполирования поверхностей по двукратным узлам:
а) n=1; х0 = 0 ; х1 = 2 ; m =2; y0 = - 1 ; y1 = 0 ; y2 =1 ;
z0,0 = 5; z0,1 = 3 ; z0,2 = 6 ; z1,0 = 8 ; z1,1 = 5 ; z1,2 = 7 ;
zх0,0 = 2; zх0,1 = 1 ; zх0,2 = 0 ; zх1,0 = 1 ; zх1,1 = 2 ; zх1,2 = 0 ;
zу0,0 = - 1; zу0,1 = 2 ; zу0,2 = 3 ; zу1,0 = - 2 ; zу1,1 = 1 ; zу1,2 = 3 ;
б) n=2; х0 = -2; х1 = -1 ; х2 =1; m =2; y0 = 0; y1 = 1; y2 =2 ;
z0,0 = -8; z0,1 = -10 ; z0,2 = z1,0 = -7 ; z1,1 = -5 ; z1,2 = -2 ; z2,0 = -5 ; z2,1 = -2 ; z2,2 =1 ;
zх0,0 = 0; zх0,1 = 1 ; zх0,2 = 2 ; zх1,0 = 1 ; zх1,1 = 2 ; zх1,2 = zх2,0 = 1 ; zх2,1 = zх2,2 = 2 ;
zу0,0 = -1; zу0,1 =1 ; zу0,2 =3 ; zу1,0 = 0 ; zу1,1 =1 ; zу1,2 =0 ; zу2,0 = zу2,1 =1 ; zу2,2 =2.
9. Написать программу, рекурсивно вычисляющую для заданного m последовательность чисел сочетаний С0 m ,
С1 m , С2 m ,…, Сm-1 m , Сm m.
10. C помощью программы bez_2d смоделировать плоские кривые, близкие по форме к а) цифре “8”, б) цифре “3”, в) цифре “6”, г) букве “с”, д) букве “е”, д) букве “s”.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.