Исследование временных характеристик линейных звеньев

2 ЛАБОРАТОРНАЯ РАБОТА № 2. ИССЛЕДОВАНИЕ ВРЕМЕННЫХ ХАРАКТЕРИСТИК  ЛИНЕЙНЫХ  ЗВЕНЬЕВ

2.1 Цель работы

Исследовать динамические свойства и определить параметры передаточных функций звеньев по временным характеристикам.

2.2 Краткие теоретические сведения

               Временной характеристикой называется закон изменения выходной величины Y в функции времени t при условии, что до приложения внешнего воздействия звено находилось в покое. Временные характеристики звена зависят от свойств звена и от характера внешнего воздействия, для которого они определяются.

В лабораторной работе рассматриваются временные характеристики звеньев, представляющие собой реакцию звеньев на стандартные воздействия :

- переходная характеристика (функция) h(t) - это реакция звена на единичное ступенчатое воздействие х(t) = 1(t) ;

- импульсная переходная характеристика (функция веса) w(t) - реакция звена на единичный импульс х(t) = d(t).

Переходная функция может быть определена экспериментально или вычислена теоретически. Если исследуемое звено описывается передаточной функцией W(s), то с учетом того, что изображение ступенчатой функции L{1(t)} = , переходная характеристика

h(t) = L^-1.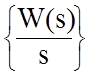

График переходной функции строится в координатах (h, t). Для линейных звеньев, при неединичном скачке входной величины Х(t) = A·1(t), выходная величина звена будет изменяться по закону Y(t) = A·h(t), где А = const.

Функция веса может быть найдена экспериментально или теоретически. Для звена с передаточной функцией W(s) с учетом того, что

L{δ(t)} = 1,

W(t) = L^-1 {W(s)}.

Если на вход линейного звена поступает неединичная дельта-функция x(t) = A·δ(t), где А = const – это площадь входного импульса, равная В·с, то реакция звена на этот импульс равна y(t) = A·W(t). График функции веса строится в координатах (W, t).

          Переход из области изображений s в область реального переменного t (время) осуществляется с помощью формулы разложения. Например, если X(s) = 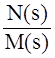, то при отсутствии кратных корней знаменателя

x(t) = ,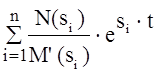

где  s_i – корни функции M(s).

При наличии кратных корней s_k, кратности n_k

x(t) = .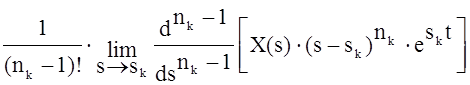

Если знаменатель имеет два одинаковых корня (n_k = 2), то

x(t) = .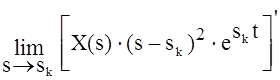

2.3 Домашняя подготовка

2.3.1Изучить материал [1, C. 40 – 64; 4, C. 42 - 88]. Обратить внимание на экспериментальное определение параметров звеньев: апериодического первого порядка [1, C. 56; 4, C. 74, рисунок 3.11], колебательного [1, С. 60 – 61; 4, С. 85 – 87, рисунок 3.2 (г, д, е), формулы 3.96 – 3.99].

2.3.2 Используя табл. 1.1 и 1.2(см. лаб. работу №1):

- записать передаточную функцию апериодического звена первого порядка Н₁(р) и зарисовать его схемную реализацию. Получить выражения для переходной и весовой функций. Построить графики переходной и весовой функций, привести таблицу значений;

- записать передаточную функцию апериодического звена второго порядка, представленную в виде последовательного включения Н₁(р), Н₂(р) и зарисовать его схемную реализацию. Получить выражения для переходной и весовой функций. Построить графики переходной и весовой функций, привести таблицу значений;

- записать передаточную функцию колебательного звена Н₄(р) и зарисовать его схемную реализацию. Получить выражения для переходной и весовой функций, построить графики, привести таблицу значений.

Примечание. При вычерчивании графиков временных характеристик масштаб по вертикальной оси принять равным (0,2 ÷ 0,1) . По горизонтальной оси (время t) масштаб взять равным (0,5 ÷ 0,25)  - для звеньев Н₁(р) и Н₁(р)· Н₂(р), и равным (1,0 ÷ 0,5)  - для колебательного звена Н₄(р).

2.4  Методические указания к выполнению  работы

2.4.1 Зарисовать осциллограмму ступенчатого сигнала 1(t) и занести его уровень U_ВХ в таблицы 2.1 и 2.2.

2.4.2 Поочередно подать сигнал 1(t) на звенья Н₁(р), Н₁(р)· Н₂(р), Н₄(р), зарисовать осциллограммы на выходе этих звеньев. Все (четыре) осциллограммы расположить друг под другом, синхронизируя их по времени с входным сигналом. При снятии осциллограмм сигнал подают на оба канала осциллографа, при этом на первый канал подается входной сигнал, на второй – выходной. Для удобства осциллографирования переключателем полярности второго входа осциллографа установить наблюдаемые сигналы по обоим каналам одного знака. Масштабы для всех осциллограмм взять одинаковые: по усилению – в пределах 1 В/см; по времени – в пределах 1 мс/см. Занести в таблицы 2.1 и 2.2 установившееся значение сигнала U_УСТ и время переходного процесса t_П.П. В таблицу 2.2 занести значения периода колебаний Т_К и амплитуд двух соседних колебаний U_m1 и U_m2 относительно установившегося значения.

          Для получения переходных характеристик провести нормирование осциллограмм, т. к. уровень входного сигнала не равен единице. Параметры переходных характеристик (К, Т₁, Т_К, А₁, А₂) занести в таблицы 2.3 и 2.4.

2.4.3 Зарисовать осциллограмму импульсного сигнала δ(t), измерить его уровень U_ИМП и длительность Т_ИМП . Определить площадь импульсного сигнала S_ВХ и занести в таблицы 2.1 и 2.2.

2.4.4 Поочередно подать сигнал δ(t) на звенья Н₁(р), Н₁(р)·Н₂(р), Н₄(р), зарисовать осциллограммы на выходе этих звеньев, расположить их как указано в пункте 2.4.2. Масштаб по усилению выбрать в пределах 0,1 В/см, по времени – 1 мс/см. Занести в таблицу 2.1 наибольшее значение выходного сигнала U_m (при t = 0) и время переходного процесса t_П.П. В таблицу 2.2 занести значения амплитуд двух соседних колебаний U_m1 и U_m2 , периода колебаний Т_К и времени переходного процесса t_П.П . Провести нормирование осциллограмм с целью получения весовой (импульсной) характеристики. Параметры импульсных характеристик (Т₁, , Т_К, А₁, А₂) занести в таблицы 2.3 и 2.5.