Построение квазиразверток на основе энергетических функций, страница 3

В формуле (*) используется величина w – номинальное или равновесное расстояние между соседними узлами. В программе, в качестве этого расстояния берется рассчитанное в начале по исходной модели расстояние между каждым узлом и каждым его соседом.

Минимизация производится одним из методов ненаправленного случайного поиска. Берется определенное число случайных пробных точек (объем выборки определен 3-им параметром в файле параметров), определяется начальный минимум. Далее снова бросаются партии точек того же объема, до тех пор пока находимый минимум лучше предыдущего. 

Изменение координат x и y за одну итерацию не более максимального равновесного расстояния этого узла с кем-нибудь из соседей.

Критерий останова – либо максимальная деформация достигла заранее определенного значения, либо уменьшение энергии стало очень медленное.

4.  Результаты.

В качестве тестовой модели был взят участок сферы:

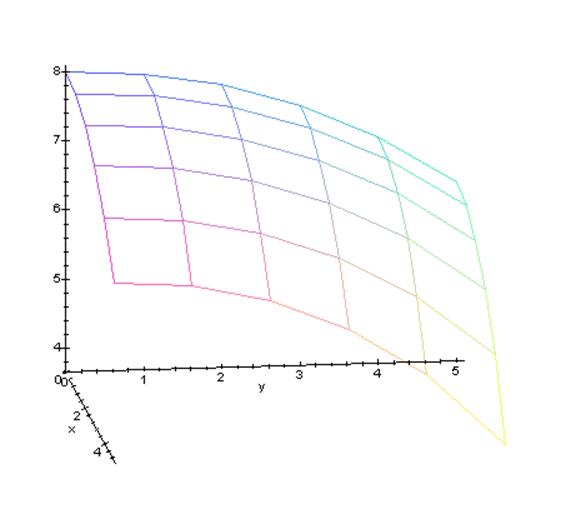
Значения параметров:

C=1000;

k=1.0;

число проб за один этап минимизации – 32000.

Исходные итоговые координаты узлов:

№

X

x

Y

y

z

z

1

0

0

0

0

8

0

2

0

-0.024081

1

0.965448

7.937254

0

3

0

-0.017257

2

1.93634

7.745967

0

4

0

-0.076576

3

2.903354

7.416198

0

5

0

-0.105191

4

3.964

6.928203

0

6

0

-0.103343

5

5.182292

6.244998

0

7

1

0.956593

0

-0.047167

7.937254

0

8

1

0.964599

1

0.988469

7.874008

0

9

1

0.948121

2

1.932683

7.681146

0

10

1

0.919875

3

2.905824

7.34847

0

11

1

0.859836

4

3.980189

6.855655

0

12

1

0.897011

5

5.199857

6.164414

0

13

2

1.904045

0

-0.063595

7.745967

0

14

2

1.930528

1

0.941817

7.681146

0

15

2

1.910143

2

1.914111

7.483315

0

16

2

1.879602

3

2.882991

7.141428

0

17

2

1.859167

4

3.948736

6.63325

0

18

2

1.852632

5

5.237389

5.91608

0

19

3

2.897207

0

-0.07824

7.416198

0

20

3

2.896706

1

0.925727

7.348469

0

21

3

2.880116

2

1.883642

7.141428

0

22

3

2.871466

3

2.868279

6.782330

0

23

3

2.881263

4

3.97476

6.244998

0

24

3

2.860832

5

5.257635

5.477226

0

25

4

3.949475

0

-0.069413

6.928203

0

26

4

3.954738

1

0.877719

6.855654

0

27

4

3.955196

2

1.884141

6.63325

0

28

4

3.950827

3

2.896192

6.244998

0

29

4

3.976239

4

3.974789

5.656854

0

30

4

3.991751

5

5.329344

4.795832

0

31

5

5.151577

0

-0.050674

6.244998

0

32

5

5.144876

1

0.9015

6.164414

0

33

5

5.17039

2

1.921321

5.91608

0

34

5

5.190533

3

2.934322

5.477226

0

35

5

5.328014

4

4.058135

4.795832

0

36

5

5.397501

5

5.451202

3.741657

0
Скачать файл