Построение квазиразверток на основе энергетических функций, страница 2

Для представления драпировки конкретной ткани нужно построить  функции энергии, представляющие изгиб и сдвиг, основываясь на системе Kawabata (система кривых и соотношений, выражающих физическое поведение тканей и используемых для классификации и установления существенных свойств различных тканей).

Общая энергия изгиба:

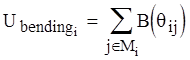, где Mi - набор шести углов, сформированных сегментами, соединяющими точку i с ближайшими соседями вдоль горизонтали и вертикали.

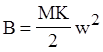
, К – кривизна;

, где M  - изгибающий момент , выражен через K, из графика Kawabata;

, w - равновесное расстояние между двумя точками;

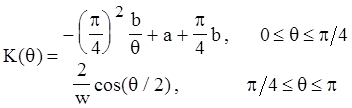
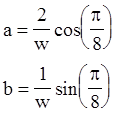
Уравнение для энергии сдвига имеет следующий вид:

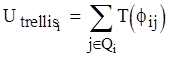
Работа dW, произведенная силой F, действующей при смещении dS есть:

dW = FdS

Если мы примем, что ширина  l образца остается постоянной во время сдвига, то путь, который проходит точка, к которой приложена сдвигающая сила, представляет собой дугу, длина которой определяется как S = l*A, где A - угол сдвига нити. Из этого соотношения получаем dS = l*dA. Если точка приложения силы движется по дуге, ее направление не совпадает с направлением силы. Fcos(A) - есть компонента силы вдоль направления смещения. Тогда мы получаем общую энергию для сдвига нитей:

Для конкретного материала, мы можем использовать кривые Kawabata для сдвигающей силы как функцию A, и проинтегрировав, получить общую энергию T.

Таким образом, мы определили внутреннюю энергию ткани на уровне частицы; с помощью предположений получили приблизительные энергетические кривые для моделирования "обобщенной ткани"; получили строгое энергетическое уравнение, основанное на структурной механике; при помощи графиков Kawabata для различных тканей получили энергетические уравнения для конкретной ткани.

3.  Практическая реализация.

Так как при построении развертки на плоскости координата Z у всех узлов сетки, аппроксимирующей микроструктуру ткани, в итоге будет равна нулю, то энергия гравитации и изгиба из формул и в соответствии с физическим смыслом также будут равны нулю.  Поиск по координате Z не проводится, эта координата сразу приравнивается к нулю,  поэтому энергии гравитации и изгиба исключены из расчета целевой функции (итоговой энергии) из-за их постоянного равенства нулю.

Вернемся к формуле расчета энергии сдвига:

**

l – ширина образца, во время сдвига с ней происходят незначительные изменения, поэтому l можно считать постоянной.

Как мы помним, F – сдвигающая сила, известна нам из графика Kawabata для конкретной материи, как функция от угла сдвига А. Для простоты расчетов в программе возможно задать линейный вид функции, а так как обычно в графиках Kawabata ноль А приходится на ноль F (это очевидно по физическому смыслу), то в расчет берется только коэффициент перед А.

F=k*A;

Таким образом, функцию (**) легко свести:

Входные данные для программы составляют:

1.  Координаты исходной фигуры (узлов сетки).

2.  Количество соседей для каждого узла (2, 3 или 4).

3.  Перечисление номеров соседних узлов для каждого узла.

4.  Тип каждого узла (узел 2-го типа – имеющий 3 соседа, 2 из которых – по координате x, т. е. левый и правый; 1-го – все остальные).

5.  Общие параметры: С – коэффициент, устанавливающий величину отталкивания и силу натяжения;  k – коэффициент, устанавливающий линейную зависимость между величиной сдвигающей силы F и углом изгиба нити при сдвиге, выраженную из графика Kawabata; количество проб за один раз – при минимизации целевой функции (максимально 32000).

Данные 1 хранятся в файле coords.dat, данные 2 в num_s.dat, данные 3 в sosedi.dat, данные 4 в type_s.dat, данные 5 в params.dat. Выходные данные – координаты узлов на плоскости заносятся при завершении работы программы в файле results.dat. Образцы файлов можно посмотреть в приложении 2.