Построение квазиразверток на основе энергетических функций

Тема: «Построение квазиразверток на основе энергетических функций».

Оглавление.

1.  Постановка задачи....................................................................................... 3

2.  Теоретическое обоснование......................................................................... 3

3.  Практическая реализация............................................................................ 6

4.  Результаты................................................................................................... 8

5.  Выводы...................................................................................................... 15

6.  Приложение 1............................................................................................ 16

7.  Приложение 2............................................................................................ 35

8.  Приложение 3............................................................................................ 43

9.  Приложение 4............................................................................................ 57

1.  Постановка задачи.

Отображение различных поверхностей на плоскость – типичная задача инженерной графики. Формулируется она следующим образом. Для заданного сегмента поверхности требуется найти плоскую область такой формы, чтобы из нее путем деформации можно было получить исходный сегмент. На деформацию обычно накладываются ограничения, обусловленные, как правило, свойствами материала, из которого предстоит изготовить объект заданной формы. Такие отображения называются квазиразвертками.

2.  Теоретическое обоснование.

Для определения микроструктуры ткани используем аппарат энергетических функций. В качестве базовой модели используем модель частиц. В этой модели будем выражать различные взаимодействия между частицами ткани на микроскопическом уровне. Представлять все детали нитевой структуры тканого материала не является ни желательным, ни принятым в вычислительной практике, но мы можем попытаться определить наиболее важные взаимодействия. Представим модель ткани как систему частиц, которые размещены в точках пересечения продольных и поперечных нитей ткани. В этой модели, мы, с помощью функций энергии, дающими простые геометрические соотношения между находящимися в непосредственной близости частицами, представляем различные ограничения и взаимодействия, происходящие на уровне нити.  Основные взаимодействия, которые происходят на уровне нити это:

1)  контакт;

2)  растяжение;

3)  изгиб;

4)  сдвиг (решеточное взаимодействие)  - наиболее сложное из взаимодействий, когда нити изгибаются в виде буквы S.

Общая энергия затем может быть определена как

Utotal = Urepel + Ustretch + Ubend + Utrellis + Ugravity , где Urepel - искусственно введенная энергия отталкивания для обеспечения условия, что имеется минимальное расстояние между частицами, предотвращающее самопересечение ткани;

UStretch - энергия, которая соединяет каждую частицу с ее 4 соседями и представляет собой силу натяжения;

UBend  - энергия, обусловленная изгибом нитей относительно плоскости окружающей ткани;

UTrellis - энергии, обусловленная изгибом вокруг нити в плоскости пересечения. Эта часть энергии обусловливает S форму нити. На макроскопическом уровне это - сдвиг, имеющий место в ткани;

UGravity - гравитационная потенциальная энергия обусловлена сконцентрированной массой частицы.

Рассмотрим энергетические составляющие и получим математическую формулу для каждого из них.

Функции натяжения и отталкивания вместе создают крутую энергетическую яму, которая и поддерживает соседние, соединенные четырмя связями частицы на номинальном расстоянии w (это - то, что предотвращает самопересечение ткани).

R(ri,j) =     C[(w-rij)5/rij]              ,ri, j <= w

*

0                               ,ri, j > w

S(ri,j) =        0                               ,ri,j <= w

C[((rij - w)/w)5]        ,ri,j > w

,где C - коэффициент, который устанавливает величину отталкивания и силы натяжения, а i, j - две последовательных точки.

Для точки i, Urepeli находится суммированием по всем точкам ткани, что можно записать как

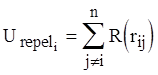
Нам нужно суммирование по соседним четырем точкам, поскольку функция спадает до нулевого значения в не близлежащих точках (это следует из определенных условий для расстояний > w).

Ustretch находится следующим образом:

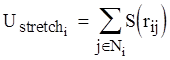
,где Ni - система четырех связанных соседей частицы i. Вместе, функции отталкивания и натяжения дают ограничение на расстояние между соседними частицами.

Энергия частицы, обусловленная силой тяжести определяется как

Ugravityi = mi g hi, где mi - масса, hi - высота частицы, и g - ускорение силы тяжести. Что касается выбора массы, мы должны брать сконцентрированную в данной точке массу ткани.