Изучение встроенных функций root(), polyroots(), Given-Find(). Решение системы нелинейных (линейных) уравнений

Лабораторная работа №4

Вариант №9

Цели работы:

- изучить встроенные функции root(), polyroots(), Given-Find().

- найти корни нелинейных уравнений с одной переменной.

- найти корни полинома.

- решить систему нелинейных уравнений.

- решить систему линейных уравнений.

Задание №1:

Решить два нелинейных уравнения с точностью до 0,0001. Отобразить корни уравнений графически. Использоваться функцию root() двух форматов. Проверить корни полинома с помощью функции polyroots(). Подставить найденные корни в уравнения и оценить погрешность.

Уравнение №1:

Установим точность вычисления, изменив значение переменной TOL:

Построим график уравнения:

По графику видно, что у уравнения 3 корня.

Вычисление корней с помощью функции root() (1ый способ):

- определим саму функции

Для решения уравнения с помощью функции root() (1ый способ), нам необходимо задать начальное значение X, относительно которого будет выполняться поиск корня. Обратимся к графику, и установим эти значения.

1 корень:

	t = -2.7914

 

2 корень:

	t = 0

 

3 корень:

	t = 1.7911

 

Вычисление корней с помощью функции root() (2ой способ):

Для решения уравнения с помощью функции root() (2ой способ), нам необходимо задать промежуток, в котором будет выполняться поиск корня. Обратимся к графику, и установим этот промежуток.

1 корень:

t = -2.7914

2 корень:

t = 0

 

3 корень:

	t = 1.7911

 

Вычисление корней с помощью функции polyroots():

Создадим вектор, составленный из коэффициентов полинома:

И с помощью функции polyroots(), получим корни уравнения:

Вычисление погрешности:

Для 1 корня:

Для 2 корня:

Для 3 корня:

Уравнение №2:

Вычисление корней с помощью функции root() (1ый способ):

1 корень:

t = 0.4861

При вычислении 2го и 3го корней уравнения лучше всего воспользоваться возможностью Trace, для определения более точного начального значения аргумента.

Получили результаты:

Для второго корня: X = 2.88; Y = 0.0062142;

Для третьего корня: X = 3.82; Y = 0.029584;

Для вычисления второго корня возьмем значение x = 2.5, для третьего x = 4

2 корень:

t = 2.8846

3 корень:

t = 3.8001

 

4 корень:

t = -4.0112

 

Вычисление корней с помощью функции root() (2ой способ):

1 корень:

t = 0.4861

 

t = 2.8846

2 корень:

3 корень:

t = 3.8

 

4 корень:

t = -4.0112

 

Уравнение  не является полиномом, следовательно, для нахождения его корней нельзя использовать функцию polyroots().

Вычисление погрешности:

Для 1 корня:

Для 2 корня:

Для 3 корня:

Для 4 корня:

Задание №2:

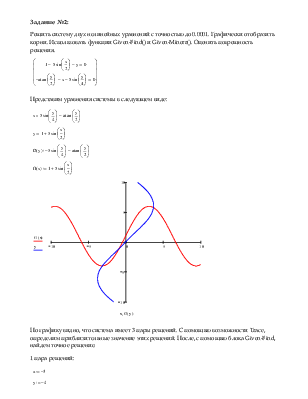
Решить систему двух нелинейных уравнений с точностью до 0.0001. Графически отобразить корни. Использовать функции Given-Find() и Given-Minerr(). Оценить погрешность решения.

Представим уравнения системы в следующем виде:

По графику видно, что система имеет 3 пары решений. С помощью возможности Trace, определим приблизительные значение этих решений. После, с помощью блока Given-Find, найдем точное решение.

1 пара решений:

2 пара решений:

3 пара решений:

Помимо функции Given-Find, можно использовать функцию Given-Minerr():

1 пара решений:

2 пара решений:

3 пара решений:

В данном случае, разницы между Given-Find и Given-Minerr нет, но в некоторых случаях функция оказывается

Вычисление погрешности:

Для 1 пары решений:

Для 2 пары решений:

Для 3 пары решений:

Задание №3:

Решить систему уравнений матричным методом и с помощью встроенной функции lsolve(). Проверку выполнить методом Крамера.

Для решения системы составим матрицу А из коэффициентов при переменных и вектор В свободных членов:

Решим систему матричным способом:

Решим систему с помощью функции lsolve():

Проверим корни методом Крамера: