Изучение форматов операторов программирования. Изучение технологии разработки программ в среде MathCAD

Лабораторная работа №7

Вариант №9

Цели работы:

- изучить форматы операторов программирования;

- изучить технологию разработки программ в среде MathCAD;

- разработать пользовательские программы в среде MathCAD;

Задание №1.

Выполнить примеры в методичке и изучить влияние исходных данных на результаты моделирования. Сделать выводы.

Пример №1

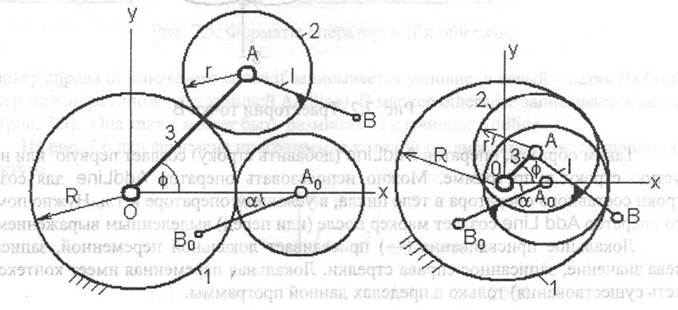
На рисунке приведена расчетная схема эпи- и гипоциклоидных механизмов. Через R и r обозначены радиусы центрального колеса и сателлита соответственно, размер стержня АВ=I. Тогда проекции точки В стержня на оси х и у декартовой системы координат (в виде вектора X) будут иметь вид:

Проекции точки В выражены в долях радиуса R центрального колеса:

Знаки «+» и «-» заменены константой к = +1 для внешнего и k = -1 для внутреннего зацепления.

Пусть имя программы S, в круглых скобках указаны передаваемые программе формальные аргументы. Кнопкой Addline созданы три строки программы, в которые записаны:

Программа S вызывается функциями F(φ) для эпициклоидных и G(φ) для гипоциклоидных механизмов.

Пример №2

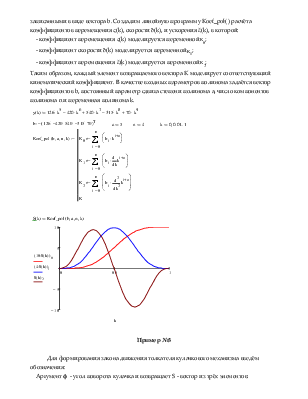
Выполним формирование закона движения толкателя кулачкового механизма с использованием функции Koef_pol( ), реализующего расчёт кинематических коэффициентов. Известно, что при синтезе кулачковых механизмов с упругим толкателем обычно подбирают такие законы его движения, при которых отсутствуют жёсткие удары. В этом случае целесообразно использовать полином седьмой степени с коэффициентами, записанными в виде вектора b. Создадим линейную программу Koef_pol( ) расчёта коэффициентов перемещения ς(k), скорости δ(k), и ускорения ξ(k), в которой:

- коэффициент перемещения ς(k) моделируется переменной;

- коэффициент скорости δ(k) моделируется переменной;

- коэффициент перемещения ξ(k) моделируется переменной;

Таким образом, каждый элемент возвращаемого вектора К моделирует соответствующий кинематический коэффициент. В качестве входных параметров полинома задаётся вектор коэффициентов b, постоянный параметр сдвига степени полинома a, число компонентов полинома n и переменная полинома k.

Пример №3

Для формирования закона движения толкателя кулачкового механизма введём обозначения:

Аргумент ϕ  - угол поворота кулачка и возвращает S - вектор из трёх элементов:

 - передаточная функция перемещения толкателя;

 - передаточная функция (аналог) скорости;

 - передаточная функция (аналог) ускорения.

Расчёт выполняется для одной из фаз толкателя:

 - фаза удаления;

 - фаза дальнего стояния;

 - фаза приближения;

 - фаза ближнего стояния.

При вращающемся кулачке угол поворота ϕ находится в интервале 0 ≤ ϕ ≤ 2π. Ход толкателя Н записывается в элемент  A₀ (A₀ = H). Таким образом, при использовании программы должен быть вначале определён вектор А, состоящий из четырёх элементов.

Пример №4

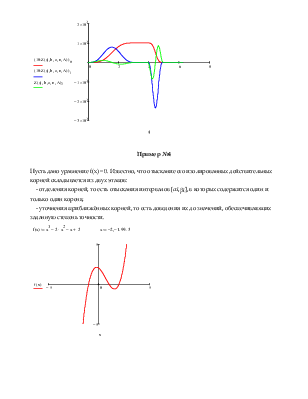
Пусть дано уравнение f(x) = 0. Известно, что отыскание его изолированных действительных корней складывается из двух этапов:

- отделения корней, то есть отыскания интервалов [αi,βi], в которых содержится один и только один корень;

- уточнения приближённых корней, то есть доведения их до значений, обеспечивающих заданную степень точности.

Пример №5

Уточнение приближённых корней, интервалы для которых найдены выше, выполняется разными методами. Рассмотрим метод половинного деления. Выбирается интервал [α,β] и находится x1. Затем проверяется условие: если , то есть на интервале [α,x1], функция f(x) поменяла знаки, то интервал [x1,β] отбрасывается и x1 становится β. Если условие  не выполняется, то есть на интервале [α,x1] функция f(x) не поменяла знаки, то отбрасывается интервал [α, x1] и x1 становится α. Вычисляется новое значение x1 и процесс повторяется.

Входными параметрами являются: описание функции f( ), вектор интервалов v, возвращаемый программой отделения корней и заданная степень точности eps.

Пример №6

Программа расчёта эвольвентной функции inv(α)=tg(α) – α работает в двух режимах. В первом режиме (k=0) вводимый параметр α моделирует угол в радианах