Основные понятия теории управления., страница 6

Что будет происходить в системе при случайных внешних воздействиях? Например, помимо подводящего трубопровода добавят жидкость в бак так, что уровень поднимется до 5 без изменения положений регулирующих органов. Подвод останется на прежнем уровне, а отвод увеличится в соответствии с расходной характеристикой и будет повышенным до тех пор, пока уровень не вернется к расчетному значению. Аналогично при уменьшении уровня в баке отвод уменьшится, и система будет стремиться к восстановлению равновесия. Таким образом, система является статически устойчивой, хотя количество отводимой жидкости не будет постоянным в течение переходного процесса.

Попытаемся улучшить характеристики системы так, чтобы количество отводимой жидкости соответствовало всегда задаваемому значению М (т.е. нагрузке). Например, добавим поплавковый регулятор уровня таким образом, чтобы среднее положение арматуры на подводе соответствовало расчетному уровню жидкости в баке φ₀.

Составим математическое описание энергетического баланса в полученной системе. Характеристика подвода будет иметь вид:

q_под = f(ξ , Δφ)

q_от= f(λ , φ)

При постоянной нагрузке и постоянном положении регулирующей арматуры на подводе (ξ=const) и на отводе (λ =const), если принять линейной зависимость расхода от положения регулирующей органов 

q_под = к_под·Δφ = к_под·(φ₀- φ)

 

где к_под  и к_от  - коэффициент статической характеристики объекта по стороне подвода и к_от  - коэффициент статической характеристики объекта по стороне отвода.

По взаимному расположению характеристик подвода и отвода т.е. по величине и знаку к_под  и к_от , можно судить, обладает ли система статической устойчивостью.

В.И. Крутовым предложена количественная мера статической устойчивости объекта, которую он назвал «фактором устойчивости»:

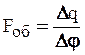
Δq = Δq_отв - Δq_под

Если F_оь > 0, объект обладает статической устойчивостью

 

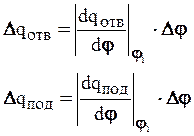
В рассматриваемом случае

Δq_под = - к_под·Δφ

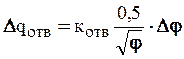
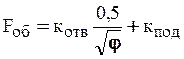
Т. к. к_под  и к_от  - положительные числа, объект будет обладать статической устойчивостью.

5.  Математическое описание САУ. Динамические звенья.

Система управления в любой момент времени производит преобразование входного сигнала  x(t) в выходной сигнал y(t).

Для математического описания системы целесообразно представить ее в виде совокупности простых звеньев, называемых динамическими звеньями.

Динамическое звено – это элемент системы, имеющий только один входной параметр x(t) и один выходной y(t) и характеризуемый определенной однозначной зависимостью

y(t) =f[x(t)]

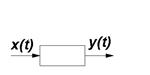
Совокупность динамических звеньев, соответствующих действию САУ или ее части, называется структурной схемой.

5.1 Типы динамических звеньев

По уровню реакции на время все динамические звенья делятся на порядки.

Звено нулевого порядка – если выходной сигнал мгновенно отслеживает входной сигнал. Зависимость между входным и выходным сигналом не включает никаких членов, зависящих от времени и может быть записана в видe формулы :

x = ky

Пример звена нулевого порядка – потенциометр, линейное перемещение ползунка которого мгновенно изменяет напряжение на выходе. Другим примером звена нулевого уровня является рычаг (рис 8).

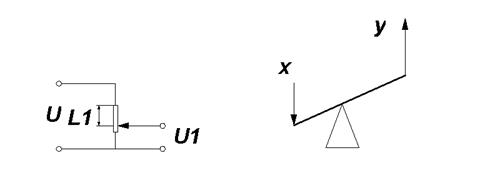
Рис. 8. Примеры звеньев нулевого порядка

Для звеньев первого порядка отношение выходного сигнала к входному зависит от скорости изменения выходного сигнала:

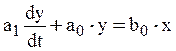
Примером звена первого порядка является термометр, показывающий температуру Т₀ и погруженный в среду с температурой Т₁.

Динамическое звено считается звеном второго порядка, если зависимость между входным и выходным сигналом имеет вид:

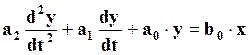
Примером системы второго порядка является пружинная система с демпфированием (рис.9).   

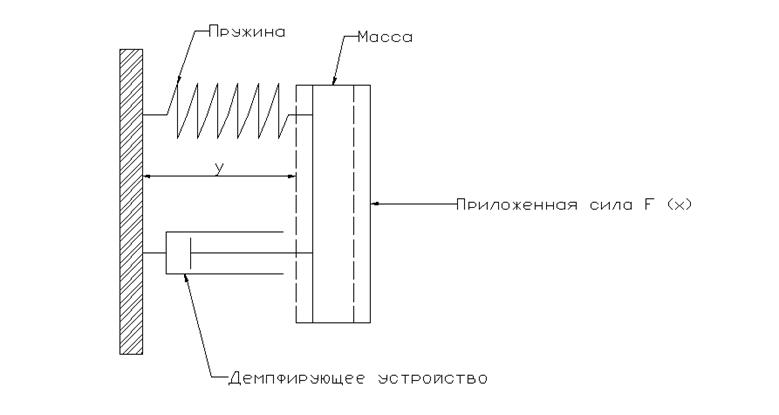
Рис.9

Система включает три основных элемента: массу, пружину и демпфирующее устройство – поршень, перемещающийся в цилиндре, заполненном маслом.