Необходимость в управлении значениями координат возникает в том случае, когда нормальный ход процесса возникает из-за различного рода возмущений, т.е. колебаний нагрузки, воздействий внешней среды или внутренних помех.
Пусть φ={ φ 1, φ 2, .. φ n} – совокупность управляемых координат процесса. В схеме, изображенной на рис 1а объект представлен прямоугольником, а управляемые координаты (выходные величины объекта) – одиночными стрелками, если они скалярные величины, или двойными при изображении вектора .
Возмущающие воздействия обозначены в виде значений λ ={λ1, λ2 , . λ n}. Управляющие воздействия показаны в виде значений ξ = { ξ1, ξ 2, .., ξ m}, прикладываемых к управляющему органу УО, с помощью которого можно изменять координаты . Величины , ξ и λ в зависимости от природы объекта связаны различными математическими зависимостями. В общем случае
φ =A(λ, ξ), где A – оператор, определяющий вид зависимости.
В простейшем случае, когда это обычная функциональная зависимость φ =F(λ, ξ), объект называют статическим или безинерционным, а зависимость φ = F(λ, ξ) или ее графическое изображение – статической характеристикой объекта (рис. 1,б).
Если объект обладает инерцией, изменение координат под воздействием возмущений λ происходит не мгновенно, и в этом случае объект называют динамическим. Величины φ, u и λ в динамических объектах связаны дифференциальными, интегральными или разностными уравнениями.

Рис. 1а Рис. 1б
Изменения координат в нормальном требуемом ходе процесса определяются совокупностью правил, предписаний или математических зависимостей, называемой алгоритмом функционирования системы. Алгоритм функционирования системы составляется на основании технологических, экономических и других требований без учета динамических искажений. В теории автоматического управления алгоритм функционирования системы считают заданным.
Алгоритм управления будет зависеть как от алгоритма функционирования, так и от динамических свойств системы.
Зная статические и динамические свойства системы управления (т.е. свойства объекта и средств управления), можно построить математическую модель системы и найти алгоритм управления, обеспечивающий заданный алгоритм функционирования при известных, задаваемых в качестве исходных данных воздействиях.
Однако модель всегда приближенно описывает систему, а возмущающие воздействия могут изменяться не известным заранее способом. Поэтому полученный таким образом алгоритм управления не всегда обеспечивает выполнение заданного алгоритма функционирования.
В сложных системах алгоритм управления увязывают не только со свойствами системы и алгоритмом функционирования, но и с фактическим состоянием системы в процессе функционирования.
В настоящее время в технике используют три фундаментальных принципа управления:
- разомкнутого управления
- компенсации
- обратной связи
Принцип разомкнутого управления: алгоритм управления вырабатывается только на основе заданного алгоритма функционирования и не контролируется другими факторами – возмущениями или выходными координатами процесса.
Принцип разомкнутого управления применим в системах любой сложности, если возмущающие воздействия не оказывают заметного воздействия на ее работоспособность.
Например, экосистема Земли для населения является разомкнутой системой управления, т.к. до последнего времени результаты хозяйственной деятельности человека компенсировались самовосстановлением флоры и фауны, водного режима и состава атмосферы.
Общая функциональная схема системы показана на рис. 2
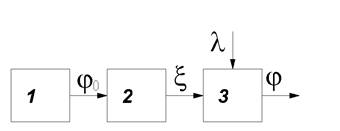
Рис. 2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.