Звездообразные (радиальные) двигатели

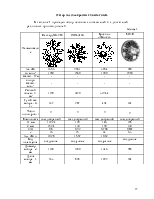
случае звезд с центральными шатунами силы инерции 2-го порядка уравновешиваются сами собой отдельно у каждой звезды, за исключением трехцилиндровой.

В случае прицепных шатунов в каждой звезде остаются неуравновешенными силы инерции 2-го порядка, которые могут образовывать пару. Величина этой пары зависит от взаимного положения главных шатунов в передней и задней звезде.

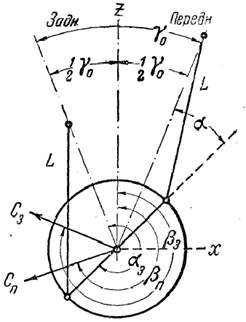
Рисунок 2.1

Допустим, что главный цилиндр задней звезды сдвинут по отношению к главному цилиндру передней звезды на угол γ₀ (рисунок 1.1). На рисунке ось координат z, общая для обеих звезд, помещена симметрично по отношению к этим главным цилиндрам.

Ранее было доказано, что в каждой звезде остаются неуравновешенные силы инерции 2-го порядка, равные

При α=0 эта сила совпадает с плоскостью кривошипа и направлена в его противоположную сторону, при вращении кривошипа она вращается с двойной угловой скоростью коленчатого вала.

Принимая это во внимание, отложим силы по их направлению, действующие в каждой звезде при расположении кривошипов, показанном на рисунке 1.1. Как видно из рисунка 1.1, сила инерции передней звезды С_п повернется от своего первоначального положения на угол 2α, сила инерции задней звезды С₃ — на угол

Спроектируем эти силы на оси координат:

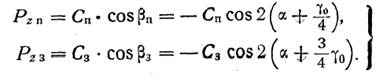
Так как обе звезды выполняются совершенно одинаковыми, можно принять С_п = С₃ = С. Суммарные силы, действующие по осям координат, будут равны

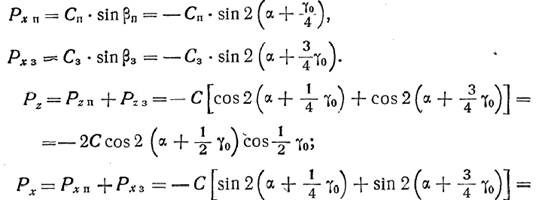
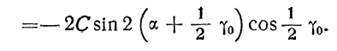
Общая равнодействующая этих сил будет равна:

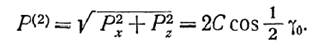
Величина этой равнодействующей будет зависеть от угла сдвига между осями главных цилиндров. При  γ_о = 0 Р⁽²⁾ = 2С; при γ_о = 90 Р⁽²⁾ = 2^0,5 С, при  γ_о =180° Р⁽²⁾ = 0.

Определим моменты, создаваемые этими силами относительно осей координат рисунок 1.2

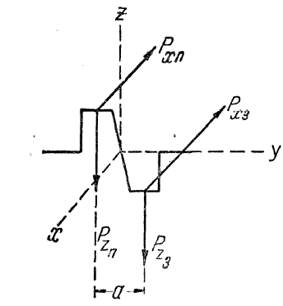
Рисунок 2.2

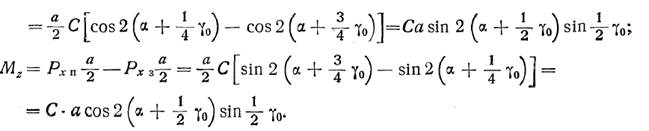
Результирующий момент будет равен:

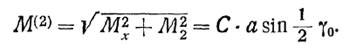
Величина этого момента также зависит от угла сдвига между осями главных цилиндров. При γ₀=0 М⁽²⁾ = 0; при γ₀=90° М⁽²⁾ = 2^0,5 Са при

γ₀=180 ° М⁽²⁾  = Са.

Следовательно, с изменением угла γ₀ меняется величина равнодействующей силы и момента.

Когда сила удваивается, что соответствует расположению главных цилиндров в затылок друг другу, момент будет равен нулю. С увеличением угла γо от 0 до 180° равнодействующая сила уменьшится до нуля, а результирующий момент растет до своего максимального значения. Результирующая сила и момент остаются неуравновешенными.

Преимущества и недостатки конструкции звездообразных двигателей.

Звездообразные двигатели содержат небольшое число движущихся деталей и имеют множество преимуществ. Они имеют небольшой вес при высокой мощности, поскольку на один кривошип коленчатого вала приходится несколько цилиндров, а картер достаточно компактен. Небольшое число движущихся  деталей, возможность обеспечения воздушного охлаждения, повышают надежность и ремонтопригодность звездообразных двигателей.

Основным недостатком звездообразных двигателей является возможность протекания масла в нижние цилиндры во время стоянки. Запуск двигателя при наличии масла в нижних цилиндрах приводит к гидроудару и поломке кривошипно-шатунного механизма. Избежать этого можно несколькими способами:

- перед запуском необходимо убедиться в отсутствии масла в нижних цилиндрах, а при его наличии слить;

- во время запуска пропускать вспышки в нижних цилиндрах, тогда масло