Многокритериальная оптимизация

Министерство образования Российской Федерации

Санкт-Петербургский  государственный горный               университет      

Многокритериальная оптимизация

По дисциплине:  Экономико-математические методы и моделирование

(наименование учебной дисциплины согласно учебному плану)

Выполнил: студент  гр. ГК-08-1412            ______________                          / Семенов С.О. /

^{(подпись)                                                   (Ф.И.О.)}

Проверил: доцент                                    ______________                                /_____________/

                                                                                                                                 ^{(подпись)                                                                                 (Ф.И.О.)}

Санкт-Петербург

2012 год

Задание:

Оценить альтернативы, характеристики которых по четырем критериям даны в таблице 1.  «Веса» критериев приведены в таблице 2, в ней также указано, что желательно сделать с данными критериями. (символ - желательно увеличить критерий, ¯- уменьшить).

1.  Построить множество решений, оптимальных по Парето.

2.  Найти оптимальные альтернативы с помощью аддитивной функции ценности. Их целесообразно искать только среди решений оптимальных по Парето.

3.  Найти оптимальные альтернативы с помощью метода главного критерия.

4.  Решить задачу, используя метод идеальной точки. Использовать метрики (S=1),  (S=2), (S=¥);

5.  Сделать окончательный вывод об оптимальной альтернативе

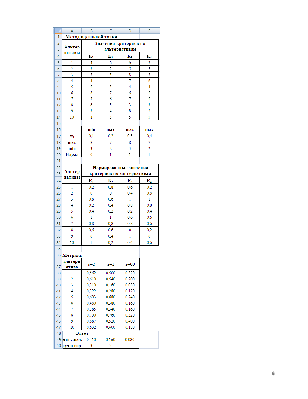
Таблица 1

Таблица 2

1.  Нахождение решений оптимальных по Парето

В результате сопоставления 10 вариантов альтернатив по четырем критериям К1, К2, К3 и К4 был сделан вывод, что невозможно однозначно сказать какие альтернативы лучше других.

2.  Аддитивная функция ценности

Линейная функция  ценности: 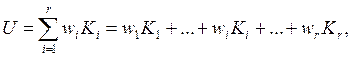       где i- индекс критерия оптимальности, i=1,2,.. r;

      w_i – вес (важность) i-го критерия.

1) Обычно используются относительные веса, т.е. 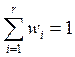 . Они устанавливаются для соизмерения  различных целей и показывают взаимоотношения между шкалами критериев.

2) K_i- значение i-го критерия. В связи с тем что у всех критериев разная размерность, то целесообразно от значений частных критериев перейти к нормированным значениям. 

Нормированные значения вычисляются по формуле:

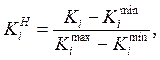
где  - соответственно максимальное и минимальное значения i-го критерия.

Знаменатель данной формулы -  длина шкалы, а числитель – положение критерия на ней. В этом случае значения нормированных критериев лежит  между  0 и 1 (см. таблицу 3).

Таблица 3