Многокритериальная оптимизация, страница 2

Альтернативы	Нормированные значения критериев по альтернативам
	К1	К2	К3	К4
1	0,2	0,8	0,6	0,2
2	0	0	0,4	0,6
3	0,8	0,6	1	1
4	0,2	0,4	0,8	0,8
5	0,4	0,2	0,2	0,4
6	1	1	0,6	0,6
7	0,8	0,8	0,8	0,6
8	0,6	0,6	0	0,2
9	0	0,4	1	0
10	1	0,2	0,4	0,6

В функциях ценности учитывается знак критерия, поэтому первый критерий (учитывающий отрицательные свойства продукции), входит в функцию ценности со знаком «минус».

 

Как видно, наивысшую ценность имеет альтернатива 3. Отрицательные значения ценности не принимаются во внимание, т.к. интерес представляет только сравнительная ценность альтернатив. Наличие отрицательных значений еще раз показывает условность функции ценности, отсутствие у неё в большинстве случаев реального экономического и технологического смысла.

3. Метод главного критерия

В методе главного критерия в качестве целевой функции выбирается один из функционалов, в нашем случае . Остальные требования к результату, описываемые критериями , учитываются с помощью введения необходимых дополнительных ограничений, т.е., решается однокритериальная задача вида:

В данном случае новое допустимое множество , будет состоять  из вариантов (3,4 и 7). Вариант 1 не вошел в это множество, поскольку значение 4-го критерия, равное 3, для него ниже допустимого уровня 5; вариант 2 – значение 3-го критерия равно 5, при допустимом 6, и т.д.

Из вариантов 3,4 и 7 выбирается тот, где K₂ максимально, это вариант 7. Следовательно, 7-ой вариант является оптимальным при заданных уровнях значимости и данном главном критерии.

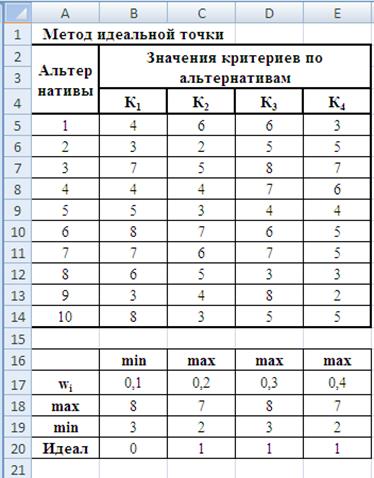
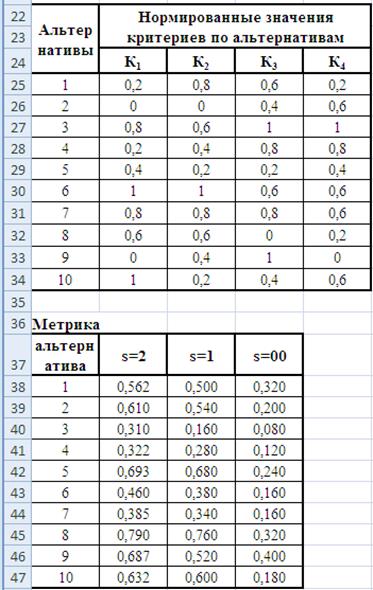
4. Метод идеальной точки

В качестве идеальной точки используется точка с наилучшими значениями критерия. Ее координаты равны 1 – для критериев, которые желательно увеличить, и 0 – для критериев, которые желательно уменьшить.

° При S = 2 расстояние до идеальной точки считается по формуле:

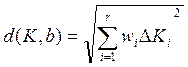, где - разность идеального и реального значений i-ому критерию

° При S = 1 задача сводится к минимизации суммы модулей относительных (с учетом «веса») отклонений.

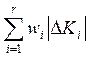
° При S = ∞ задача сводится к минимизации максимального относительного отклонения, т. е. 

       

Метод решения многокритериальных задач путем определения меры близости решения к некоему идеальному (так называемой точке идеала, или идеальной точке), т.е. решение должно обеспечивать наибольшее приближение к множеству одновременно недостижимых целей.

Данный метод используется при различных метриках, функциях расстояния.

● При  S =2   вычисляется евклидово расстояние: d(K,b) =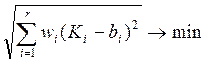

b - r-мерный вектор, характеризующий идеальную точку, т.е. включающий желатель       ные (идеальные) значения отдельных критериев;

d – расстояние между K и b (т.е. между критериями, характеризующими полученное и                      идеальное решения), определенное на основании какой-либо метрики.

● При S= 1 задача сводится к минимизации суммарного модуля относительных (с учетом «веса») отклонений:

● При S = имеем равномерную метрику, и задача целевого программирования сводится к минимизации максимального относительного отклонения, т.е. -имеем минимаксную целевую функцию.

Выводы: на основе решений с помощью аддитивной функции ценности и используя метод идеальной точки, получилась оптимальная альтернатива 3, а с помощью метода главного критерия – 7.  Но так как метод главного критерия является субъективным в определении допустимых уровней, то оптимальной альтернативой данной задачи является 3-я.