Оценика альтернативы, характеристики которых выражены в четырех критериях

Задание№2.

Постановка задачи.

Оцените альтернативы, характеристики которых по четырем критериям даны в таблице 1. «Веса» критериев по вариантам приведены в таблице 2. В последней таблице также указано, что желательно сделать с данным критерием.

Требуется:

1.  Построить множество решений оптимальных по Парето.

2.  Найти оптимальные альтернативы с помощью аддитивной функций ценности . Их целесообразно искать среди решений оптимальных по Парето.

3.  Найти оптимальные альтернативы с помощью метода главного критерия. В таблице символом* отмечен главный критерий.

4.  Решить задачу, используя метод идеальной точки. Использовать метрики (S =1), (S = 2), (S=¥).

5.  Сделать окончательный вывод об оптимальной альтернативе.

Исходные данные для решения задачи.

Таблица №1

Альтернативы		Критерии
	К1	К2	К3	К4
1	4	6	6	3
2	3	2	5	5
3	7	5	8	7
4	4	4	7	6
5	5	3	4	4
6	8	7	6	5
7	7	6	7	5
8	6	5	3	3
9	3	4	8	2
10	8	3	5	5

                                                 Таблица №2.

Вычисления:

1.  Построим множество решений оптимальных по Парето.

Вектор значений показателей К* из области допустимых значений называют эффективным или оптимальным по Парето, если не существует другой такой точки в области допустимых значений, которая по всем параметрам была бы не хуже К^* и превосходила его хотя бы по одному.

Выделение решений, оптимальных по Парето, позволяет сократить количество рассматриваемых альтернатив.

Сопоставим десять альтернатив по двум критериям К₁ и К₄, которые нам нужно минимизировать. На рисунке 1 представлена геометрическая интерпретация альтернатив.

Рис.1.

 

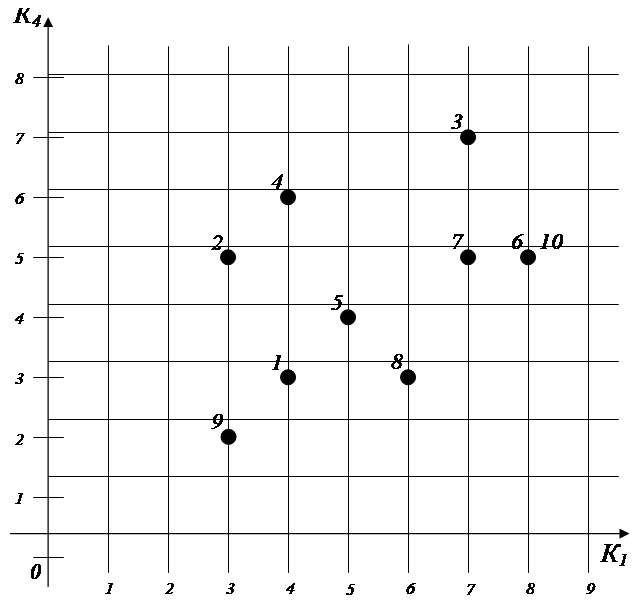Альтернативы, 1, 2, 5, 8, 9 являются оптимальными по Парето, так как по обоим критериям лучше их нет. В то же время альтернативы: 3, 4, 6, 7, 10 не входят в множество Парето.

Сопоставим десять альтернатив по двум критериям К₂ и К₃, которые нам нужно максимизировать. На рисунке 2  представлена геометрическая интерпретация альтернатив.

Рис. 2.

 

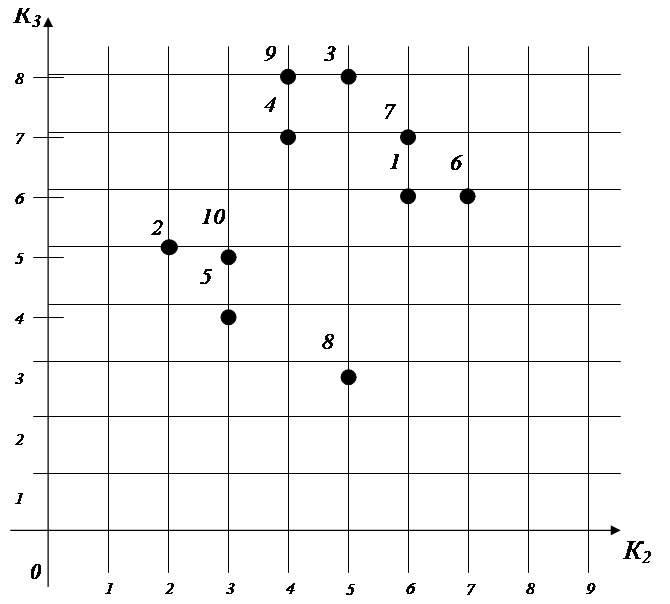Оптимальные альтернативы, которые нужно максимизировать:  1, 3, 6, 7, 9.

2. Определим оптимальную альтернативу с помощью аддитивной функцией ценности среди всех решений (рассмотрим все 10 альтернатив).

Формула для вычисления аддитивной функции:

U = 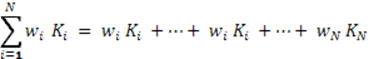, где

i- индекс критерия оптимальности, i=1, N;

 w_i – вес (важность) i-го критерия.

K_i - значение i-го критерия.

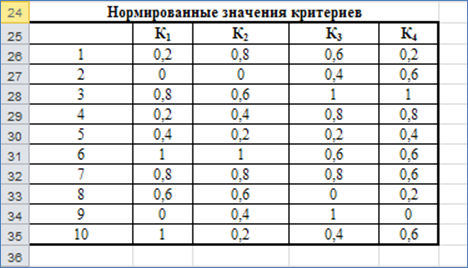
В нашем случае при вычислении аддитивной функции нет необходимости переходить к нормированным критериям, поскольку значения критериев – целые числа, т.е. будем использовать балльный метод. Результаты расчёта приведены в таблице Excel:

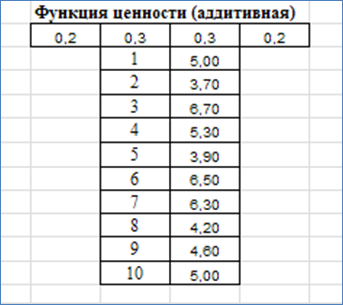
Вывод: наивысшую ценность имеет альтернативы 3 (по результатам вычисления аддитивной оценки).

3. Найдём оптимальные альтернативы с помощью метода главного критерия.

Главным критерием является К₄, а для 1-го, 2-го и 3-го критерия допустимыми уровнями будут 6, 5 и 5 соответственно. К₁  и К4 нам следует уменьшить, а К₂  и К₃ увеличить. В данном случае оптимальной альтернативой  по 1-му, 2-му и 3-му критериями будет являться 1-я альтернатива. Но по главному критерию К₄ ≤ 2 оптимальной альтернативой является 9-я.  Следовательно, 1-я и 9-я альтернатива являются оптимальными при заданных уровнях значимости и данном главном критерии.

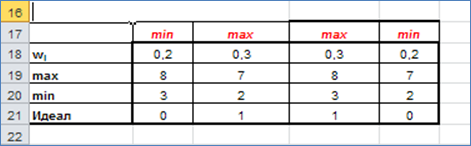
4. Произведём нормирование значений критериев по формуле:

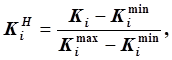
где     - соответственно максимальное и минимальное значения i-го критерия.

Знаменатель данной формулы, длина шкалы, а числитель – положение критерия на ней. В этом случае значения нормированных критериев лежит  между  0 и 1.

Найдем альтернативу наиболее близкую к идеальной точке, определяемой наилучшими значениями каждого из критериев.

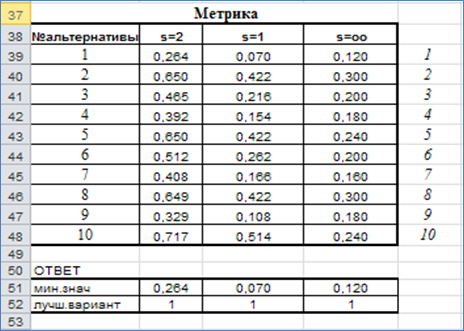
Вывод: Для трёх различных метрик лучшим вариантом является альтернатива 1.