Многокритериальные задачи

МНОГОКРИТЕРИАЛЬНЫЕ ЗАДАЧИ

Математические модели, формализующие свойства определенной производственной ситуации, позволяют получить строгое оптимальное решение при конкретной, четко поставленной цели, описываемой единственным критерием оптимальности.  Возможные варианты решения обычно оцениваются с различных точек зрения. Как правило, имеется, несколько целей и соответствующие им критерии оптимальности. На практике однокритериальные задачи встречаются редко, реальным является наличие  у человека или организации задачи, которую оценивают одновременно несколько критериев.

Например, сложной многокритериальной задачей являются выбор проектного (технического) решения строительства горного предприятия, где наряду с экономическими показателями следует учитывать вопросы надежности и безопасности, трудность эксплуатации и строительства, сроки осуществления проекта.

Другие сложные многокритериальные задачи - оценка работы предприятий, размещение  объектов жилой застройки, подбор кандидата на должность, распределение средств (ассигнований на научные исследования, капитальных вложений, фонда развития производства и др.) между различными объектами и т.д.

В этих случаях необходимо указать систему величин, характеризующих качество каждого из возможных решений:

                                                                  (1)

где  Z - пространство переменных,

z – переменные модели,

r- количество критериев.

Такая запись условна: в  отличии от обычной оптимизационной задачи (r=1), в которой было необходимо найти  максимизирующее значение единственного показателя, в многокритериальном случае  такая запись означает лишь, что желательным является увеличение каждого из показателей (при неизменном значении других). Т.о. возникает проблема оптимизации принимаемых решений сразу по нескольким критериям. Эту проблему решают с помощью теории выбора и принятия решений.

Отличительная особенность многокритериальных задач - наличие неопределенности, связанной с необходимостью сопоставления решений по нескольким критериям.

Пример 1.

Имеется 4 участка под  индивидуальную жилую  застройку.

Необходимо  по фактическим значениям критериев  имеющихся участков определить их предпочтительность. В число критериев входят:

1.  Расстояние от городской черты;

2.  Привлекательность застройки (живописный ландшафт, наличие исторических памятников);

3.  Инженерно-транспортная структура (расстояние до ближайшего подключения к линии электропередач,  развитость транспортных сетей).

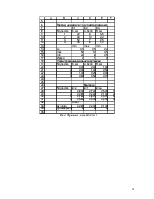
В табл.1 приведены значения критериев. Очевидно, что первый  и третий критерии желательно минимизировать, второй – максимизировать.

Таблица 1.

В данном примере, анализируя предложенную таблицу, заметим, что в ней отсутствует вариант одновременно наилучший по всем критериям (так называемый, доминирующий).  Вариант № 1 - наилучший по первому критерию (S ), № 2 - по второму (A) и № 3 - по третьему (). Вариант 4 не является оптимальным ни по одному из критериев, но по всем из них стоит на втором месте, т.е. компромиссный.

Обычно решение задачи многокритериальной оптимизации заключается