Направления и концепции современного естествознания, страница 4

С именем Больцмана связано истолкование 2-го закона термодинамики и энтропии. Он ввёл в физику статистические методы и рассмотрел распределение молекул по состояниям (координатам, импульсам, энергиям). В частности, распределение молекул по энергиям устанавливается следующей формулой:

, где

 — начальное состояние молекул в объёме,

 — постоянная Больцмана,

 — полная энергия молекул,

 — температура.

Больцман установил некое наивероятнейшее состояние среды и связь энтропии с вероятностью состояния :

                                                                 (4)

 — число способов, с помощью которых можно осуществить данное состояние.

Физики неоднократно оспаривали эту формулу, но последующее развитие науки подтвердило её справедливость.

Пример (случай устойчивой системы)

Реализуется одно состояние:

 .

Пример  — число способов, которыми можно разместить молекулы газа в сосуде, т. е.  — есть мера неопределённости и хаотичности системы.

Постоянная Больцмана  энтропийных единиц.

.

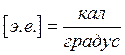Энтропия пропорциональна массе:

            

            

Больцман фактически ответил на вопрос о физическом смысле энтропии и причинах её роста в изолированных системах. Энтропия — это мера беспорядка в системе (порядок соответствует минимуму энтропии), т. е., если система предоставлена сама себе (она изолирована), то коллектив частиц стремится перейти в состояние, в котором при данных условиях возможен полный хаос (ему соответствует максимум энтропии).

Пример В кристаллическом твёрдом теле энтропия меньше, чем в жидком.

Связь между вероятностью состояния системы и энтропией Больцман показал на простом примере. Известно, что , следовательно, энтропия всей системы равна сумме составляющих. По теории вероятности вероятность данного состояния вещества полной системы равна произведению вероятностей её составных частей. Такими свойствами обладает .

                                                                 (1)

Изменение энтропии в открытых системах

Если посмотреть на биологическую систему через призму второго закона термодинамики, то на первый взгляд есть парадокс: процессы жизнедеятельности нарушают принципы термодинамики.

Система при росте совершенствуется и упорядочивается. Однако  увеличивается необратимым самопроизвольным образом, происходящем в изолированных системах. Биологические системы — открытые.

Наша задача:

• Понять, как связаны изменения энтропии с параметрами процессов в открытой системе.
• Выяснить, можно ли предсказать общее направление необратимых процессов по изменению энтропии в открытой системе.

Главная трудность в том, что необходимо учитывать изменение всех термодинамических параметров во времени непосредственно в ходе развития процессов в открытой системе.

В 1945 Пригожин показал, что изменение энтропии в неизолированной системе, обменивающейся с внешней средой энергией и веществом, представляется в виде:

,

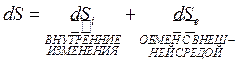 — обусловлена приростом энтропии за счёт необратимых процессов внутри системы (производство энтропии);

 — обусловлена происходящим обменом с окружающей средой.

Производство энтропии обусловлено диссипативными процессами (теплопроводность, диффузия, вязкость …) — процессами с рассеянием энергии.

В общем случае . Если  и превышает по модулю , то на определённой стадии эволюции может происходить понижение энтропии.

Справедлив постулат Пригожина:

.

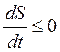Биологами установлено, что при фотосинтезе приток энергии света приводит к уменьшению энтропии клетки, а процессы дыхания, химические реакции в клетке увеличивают энтропию.

Согласно теории Шеннона (1949 год), количество информации  о единичном реальном состоянии системы подчиняется соотношению

.                                                               (2)

Попытаемся формально оценить количество информации, содержащейся в теле человека:

 бит

За бит принимается информация, содержащаяся в достоверном сообщении, когда число исходных возможных состояний .

Сопоставляя (1) и (2), можно найти связь между  и  в битах:

 э. е.