Знания в системах ИИ, страница 4

в) стратегия использования подслучаев;

2)  Стратегия очищения

методы доказательства с определенной резолюцией

3)  Стратегия упорядочения-стратегии, в которых не запрещаются никакие типы резолюции, а лишь даются указания на то какие из них нужно выполнить в первую очередь.

4)  Комбинирование - получено комбинированием нескольких стратегий  .

Стратегия, полученная на основе полной стратегии, может получиться неполной. 

24) Решить методом доказательства теоремы  с помощью принцип резолюции     следующую задачу: «Погрузочный робот (пр) находится на автоматической тележке(ат). Тележка находится на складе. Где находится автоматический робот? »

Использовать предикат Б(x,y)-быть в определенном месте. Построить граф опровержения.

Решения

Множество

1-ая формула –в каком бы месте не находилась тележка в этом же месте находится погрузочный робот.

2-ая формула –тележка находится на складе.

Задача сводится к доказательству теоремы :  

Определив , получим ответ. Т.к. есть квантор , то после нахождения доказательства теоремы можно извлечь тот частичный случай пер-й относительно квант.  ,который является ответом -док-во теоремы. К мн-ву  добавляем и все гл. рассм. мн-ва преобразуем в формулу предложений; затем с помощью принципа резолюции покажем ,что не выполняется

, то рассм. мн-во.

26. Используя принцип Уинстона для аналогии написать на прологе программу, которая решает задачу: ABCDÞBADC; NJKLÞ?

domains

figure =char*

figurelist   =figure*

pair=is_to(figure,figure)

predicates

match (figure, figure,simbol)

analogy (pair,pair, figurelist)

figures(figure, figure, figure)

answers(figurelist)

test_analogy(figure)

member(figure, figurelist)

goal

test_analogy(X), write(X)

clauses

analogy(is_to(A,B),is_to(C,X),Answers):-match(A,B,Rule),

match(C, X, Rule),

member(X, Answers).

match[A1,A2,A3,A4],[A2,A1,A4,A3], invertletters

test_analogy(X):-fugures(A,B,C), answers(Answers, analogy(is_to(A,B),is_to(C,X),

figures ([‘A’,’B’,’C’,’D’], [‘B’,’A’,’D’,’C’],[‘N’,’G’,’K’,’L’]).

answers ([[‘N’,’G’,’K’,’L’],[ ‘G’,’N’,’L’,’K’],[ ‘K’,’N’,’L’,’G’],[ ‘N’,’G’,’L’,’K’]]).

member(X,[X| Xs]):-!.

member(X,[Y| Xs]):-member(X,Xs).

27. Используя принцип Уинстона для аналогии написать на Прологе программу, которая решает следующую задачу

 

?

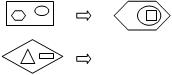domains

figure =squar; circle; triangle;

angle6; romb;

above (figure, figure);

inside(figure, figure)

figurelist   =figure*

pair=is_to(figure,figure)

predicates

match (figure, figure,simbol)

analogy (pair,pair, figurelist)

figures(figure, figure, figure)

answers(figurelist)

test_analogy(figure)

member(figure, figurelist)

goal

test_analogy(X), write(X)

clauses

analogy(is_to(A,B), is_to(C,X),Answers):-match(A,B,Rule),

match(C, X, Rule),

member(X, Answers).

match(inside(figure1,above(figure2, figure3)), ]

inside (figure2, inside(figure3, figure1)),

abovetoinsert).

test_analogy(X):figures(A,B,C),

answers(Answers),

analogy(is_to(A,B), is_to(C,X),Answers),!.

figure(inside(square,above(angels, circle)),

inside (angle6, inside(circle,square)),

inside (romb, above(triangle, square)).

answers([ inside(triangle,above(square,circle)),

inside(square,square),

inside(romb,above(triangle,square)),

inside(triangle,

inside(square,romb) )  ]).

member(X,[X| Xs]):-!.

member(X,[Y| Xs]):-member(X,Xs).