Знания в системах ИИ, страница 3

Общая схема обратного вывода:  если eq – означает отношение «подмножество» и во внутренней БД  имеются факты:

Fakt(eq (“кошка”, “млекопитающеее”)).

Fakt(eq (“собака”, “млекопитающеее”)).

Fakt(eq (“воробей”, “птица”)).

Fakt(eq (“млекопитающеее ”, “животное”)).

Fakt(eq (“птица”, “животное ”)).

Rule(eq(X, Z), [eq(X, Z), eq(Z, Y)]).

Quest(_, “что такое”).

Тогда запрос м. выглядеть так:

Inference(eq((“кошка”,   “животное ”)) 

Или

Inference(eq(“кошка”, X)).

18.Реализовать на Прологе  прямой вывод

Алгоритм:

Пока цель не доказана

Цикл   Формирование множества подходящих правил (по их условиям и наличию  фактов). Выбор одного правила из этого множества (с использованием определенной стратегии выбора). Считать текущим элементарным усл-ем – первое.

Пока  Не проверены  все элементарные усл-ия правила и не нужно прервать правила  проверку

Цикл  

Если   Элементарное усл-ие истинно  То

                                Перейти к следующему элементарному усл-ию

Иначе

Прервать проверку  усл-ия

Конец Если

Конец Цикла 

Выполнить заключения.

Если   При  формировании заключения появился целевой факт  То

Считать, что цель  доказана

Конец Если

Конец Цикла            

19. Реализовать на Прологе нечеткий вывод.

Clausses

Inference (X, K) :- fact(X, K )    

% цель выполнена если в БД есть соответствующий факт   

% с  некоторой достоверностью

Inference (X, K) :-    rule (X, Coud,  Kr ),       

% цель выполнена, если в БД есть правило,

Inference L(Coud, Kc),     % по кот. утверждение цели выводится из  

K = Kr + Kc.                     % факторов, при этом, даваемые правилом и

% утверждением, они суммируются

Inference (eq (X, Y), K) :- quest (X, Q),

Write (Q),

Read (Y, K),

Assert (fakt (eq(X, Y), K)).

Inference  L([ ], 1) :- !.

Inference  L([ X| XX ], Kc) :-Inference (X, K),           

% достоверность списка равна min - ой

Inference  L(XX, KK),  %  достоверностей  элементов списка

Min (K, KK, Kc).          % min (X, Y, X) :- X<Y,!  Min (X, Y, Y)

Kr – коэффициент уверенности, полученный ч/з правило.

Kc – коэффициент уверенности, полученный ч/з цель.

20. Реализовать на Прологе вывод с объяснениями

Там отсутствует механизм объяснения, кот. должен  отвечать на вопросы:

-  “почему задан этот вопрос”;

-  “как получено решение”.

Inference (X, [ ]): - fakt (X).  

Inference (X, [N | NN]): - rule (N, X, Coud),

Inference  L(Coud, NN).

Inference L([ ], [ ]): - !.

Inference  L([ X | XX ], HHH): - Inference (X, H),

Inference  L(XX, HH),

Append (H, HH, HHH).

% конкотенация списка

Реализуется как и обратный вывод, но для цели приводится вывод (из БД в виде факта).

21)Следующее выражение преобразовать к форме дизъюнктов (предложений) Хорна:

Решение

Исключим импликацию

продвинем внутрь отрицание

разделим переменные

заменим  на скалярную функцию , исключим .

выносим кванторы всеобщности в начало формулы

применим закон дистрибутивности

исключая кванторы всеобщности и заменяя конъюнкцию ф-я их множеством, получим множество

22)Построить граф опровержения (метод резолюции)для следующей теоремы:

Решение

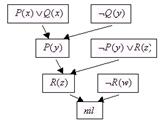23) Какие стратегии используются для сокращения вариантов перебора в методе резолюции? Приведите пример их использования.

Решение

1)  Стратегия упрощения

а) удаление тавтологий ();

б) удаление предположений с уникальными литерами;