Знания в системах ИИ, страница 2

ISA			ISA			ISA
	хордовые			птица			Птица
имеет			умеет			Умеет
	крылья			плавать			Летать
			Живет			Не умеет
				Антарктида			плавать
			Не умеет			живет
				летать			В Евразии

9. Привидите примеры фреймов –структур, фреймов-ролей, фреймов-ситуаций, фреймов-сценариев.

Фрейм-структура: займы, залоги и иерархия правительства;

Фрейм-роли: президент;

Фрейм-ситуаций: путчи, революции , бунты;

Фрейм- сценарии: пленумы, совещания.

10. Каким образом слот фрейма может получать значение?

1.  По умолчанию

2.  Через наследование

3.  По формуле указанной в слове

4.  Через присоединенную процедуру

5.  Через диалог с пользователем

6.  Через базы данных

11. Отличие фрейма -прототипа от фрейма – экземпляра

Фрейм-прототип выступает в виде шаблонов, которые содержат пустые слоты!

Фреймы-экземпляры же представляют собой конкретные объекты, слоты которых обозначенные (непустые)

12. Какие типы отношений являются обязательными для семантических сетей?

Класс – город

Элемент класса – Москва                      

 

Родовидовое отношение                             Цветок – класс

Роза – Элемент класса

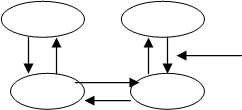
Город                     зоопарк            

Класс – представитель класса

Москва                      Моск.

зоопарк

13.  Построить семантическую сеть для примера:

У Иванова есть автомобиль “Жигули” 10-й модели красного цвета в удовл  состоянии.Автомобиль паркуется на платной автостоянке в 100 м от дома.

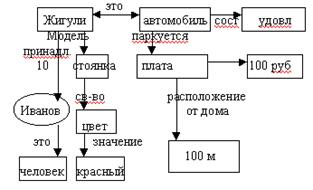14.  Построить систему правил БЗ для ситуации:

Как выбрать метод численного интегрирования для ОДУ?

15.  Почему язык Пролог удобен для решения задач ИИ?

( см. вопрос 5)

Пролог имеет мощный механизм обратных выводов (отождествление). Знания, описанные на Прологе, оснащены функциями моделирования процессов; обеспечивается редукция, индукция, импликация, аналогия и другие выводы.

16.  Отличия прямого и обратного выводов? Как при этом возбуждаются правила?  (см. вопрос 31 ) 

Прямой вывод возбуждается условием, а обратный – целью.

17. Реализуйте на Прологе обратный вывод.

Domains

Obj = eq(string, string)

Obj L =  Obj *

Database

Fakt(Obj)

Rule(Obj, Obj)                                  % rule(<действие>, <условие>)

Quest(string, string)

Predicates

Inference(Obj)

Inference(Obj, L)

Clauses

Inference(X) : - fakt(X),     % цель выполнена, если в БД есть такой факт

Inference(X) : - rule(X, Coud)

% цель  выполнена, если в БД есть пр-ло, показывающее

InferenceL(Coud)   % м. вывести утверждение цели из фактов

Inference(eq(X, Y)) : - Quest(X,Q), % пр-ло, реализующее

Write(Q),     % запрос к пользователю

Read(Y),

Assert(fakt(eq(X, Y))).

InferenceL([ ]): - !.

InferenceL([X | XX]): - Inference(X),

InferenceL(XX).