Гидравлический расчет судоходных шлюзов с распределительными системами

БАЛТИЙСКИЙ  ГОСУДАРСТВЕННЫЙ  ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ  "ВОЕНМЕХ"

им.  Д. Ф.  УСТИНОВА

Кафедра И3

Домашнее задание

по учебной дисциплине  «Методы оптимизации»

на тему  «Гидравлический расчет судоходных шлюзов с распределительными системами»

студент:        

Фомин Святослав

Группа И391 

ПРЕПОДАВАТЕЛЬ

/ Кабанов С.А.______ /

Фамилия И.О.                   Подпись

“___" _________________   г.

САНКТ-ПЕТЕРБУРГ

2012
Содержание

1. Задание. 3

2. Решение. 4

3. Решение с помощью пакета MathCad. 6

4.Результат………………………………………………………………………………………………………….10

Заключение. 11

Список использованной литературы.. 12

Задача

Установить оптимальные размеры основных конструктивных элементов питания судоходных шлюзов, и нахождение оптимального управления откачкой воды, при которых обеспечивается  опорожнения камеры за заданное время.

Уравнение системы принимает вид:

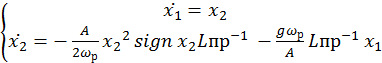
Основные конструктивные параметры:

А- приведенная площадь зеркал наполнения камеры и камеры шлюза.

А=9000

- площадь расчетного сечения подачи воды

=15…25

Lпр- приведенная к площади расчетного сечения длина водопроводных галерей

Lпр =150…300

-коэффициент сопротивления системы питания

=0.5…0.9

Решение

Основной целью при решении данной задачи являлось нахождение оптимального  управления, а также подбора характеристик основных конструктивных параметров, которые обеспечивали бы опорожнение шлюза в заданный диапазон времени при выбранных из заданного диапазона значений конструктивных параметров системы.

Ход Решения:

Примем за управление время переключения  

Тогда система примет вид:

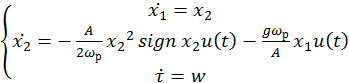        (1)

За минимизируемый примем критерий Красовского

Гамильтониан системы имеет вид:

Система сопряженных переменных:

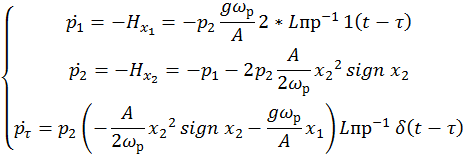
Оптимальное управление равно

w=

Для нахождения оптимального времени переключения используем алгоритм с прогнозирующей моделью:

Последовательность решения:

1.  Находится гамильтониан:

2.  Находится управление  из условия:

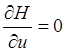
3.  Полагается:

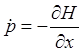      (3)

4.  Интервал оптимизации разбивается на шаги Δt.

5.  Полагается .

6.  Интегрируется в прямом времени система уравнений (1) и при w = 0 от t до . Находится .

7.  Вычисляются граничные условия для р:

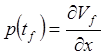
8.  Интегрируются совместно системы (1)и (3) с шагом интегрирования (-Δt) от до t. Находится р(t).

9.  Вычисляется .

10.  Интегрируются (1) при u =  на один шаг вперед.

11.  Проверка:  Если да, то Стоп

Если нет, то на шаг 6 для t = t + Δt

Решение с помощью пакета MathCad

Интегрирование системы в прямом времени

Интегрирование в обратном времени

Нахождение оптимального управления

Интегрирование системы на 1 шаг вперед с выбранным оптимальным управлением

Результат

В результате работы алгоритма при подобранных параметрах системы

А=9000

=40

Lпр =150

=0.9

получено оптимальное время переключения управления

Заключение

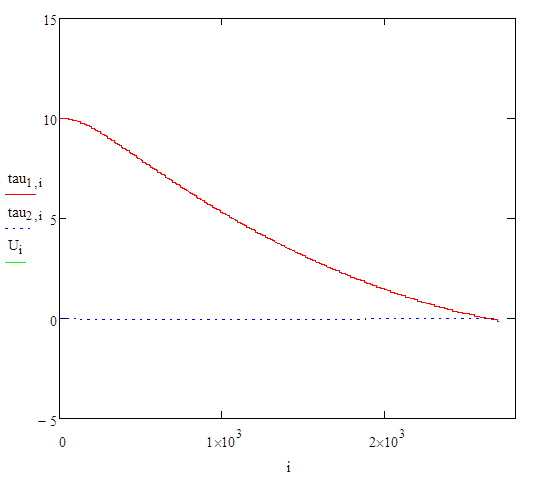
При решении задачи были подобраны оптимальные значения основных конструктивных элементов судоходного шлюза. Было получено оптимальное управление, обеспечивающее слив воды из шлюза в заданный промежуток времени при выбранных параметрах системы.

Список использованной литературы

1. Кабанов С.А. Прикладные задачи оптимального управления; Балт. гос. техн. ун-т. -СПб., 2007
2. Конспект лекций по дисциплине «Методы оптимизации».
3. Кабанов С.А. Управление системами на прогнозирующих моделях. СПб: Издательство С.-Петербургского университета, 1997.

Были получены навыки решения инженерных оптимизационных задач.