1. Определяется площадь поверхностей блока:
SВ = SН = L1·L2 - для верхней и нижней поверхностей блока:
SБ = (L1 + L2)·L3 - для боковой поверхности блока;
где
L1 - длина блока, м;
L2 - ширина блока, м;
L3 - высота блока, м;
2. Задаемся перепадом температур "корпус-среда": DtКС =10 °С.
3. Определяем температуру корпуса блока:
tк = tс + Dtкс, где tс - температура среды, °С.
4. Находим среднюю температуру между корпусом и средой:
.
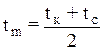5. Определяем закон теплообмена:
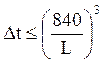, L
берется в мм.
Если данное условие удовлетворяется, то теплообмен происходит по закону 1/4, иначе – по закону 1/3.
Для закона 1/4
6. Рассчитываем коэффициенты конвективного теплообмена для каждой поверхности блока:
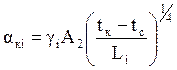
7. Определяем коэффициент лучеиспускания для каждой поверхности блока:
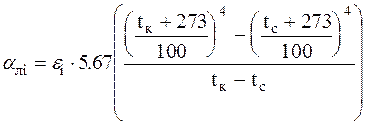
где ei - степень черноты поверхности.
8. Определяем тепловую проводимость между поверхностью корпуса и окружающей средой:
sк = (aкн + aлн) · Sн + (aкб + aлб) · Sб + (aкв + aлв) · Sв, где aкн, aкб, aкв - коэффициент конвективного теплообмена для соответственно нижней, боковой и верхней поверхности блока;
aлн, aлб, aлв - коэффициент лучеиспускания для соответственно нижней, боковой и верхней поверхности блока.
9. Рассчитываем значение перегрева "корпус-среда" во втором приближении:
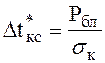, где Pбл - мощность блока,
Вт.
10. Определяем ошибку расчета:
.
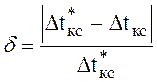Если d £ 0.05, то переходим пункту 11 первого этапа расчета.
Если d > 0.05, то переходим к пункту 3 первого этапа, считая Dtкс = Dtкс*.
11. Определяем температуру корпуса с учетом перфорации и поправки на внешнее давление:
Dt'кс = Dtкс · Ккп · КН1, где ККП - коэффициент, зависящий от коэффициента перфорации КП блока:
КН1 - коэффициент, зависящий от атмосферного давления H1 окружающей среды:
12. Определяем температуру корпуса блока:
tк = tс + Dtкс*.
На данном этапе расчет зависит от вида тепловой схемы. Может быть 6 вариантов тепловых схем.
1) Герметичный или закрытый блок, платы расположены в направляющих вертикально (ТС 1).
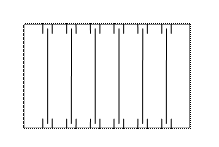
2) Герметичный или закрытый блок, платы расположены в направляющих горизонтально (ТС 2).
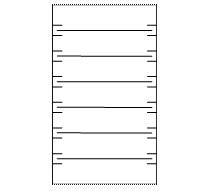
3) Герметичный или закрытый блок, платы собраны в микромодульный массив (книжная компоновка) (ТС 3).
4) Перфорированный блок, платы расположены в направляющих вертикально (ТС 4).
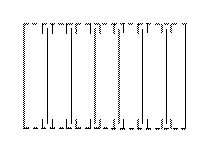
5) Перфорированный блок, платы расположены в направляющих горизонтально (ТС 5).
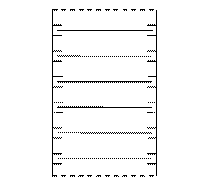
6) Перфорированный блок, платы собраны в микромодульный массив (ТС 6).
2 этап для тепловых схем ТС 1 и ТС 2.
Расчет проводится на основании закона Фурье.
1. Определяем площадь контакта между платой и направляющей:
Sконт = 2 l (b + a), где l - длина стороны платы, контактирующей с направляющей, м;
a - толщина платы, м;
b - глубина направляющей, м.
2. Определяем тепловое сопротивление зазора между платой и направляющей:
, где Кз - коэффициент, зависящий от материала
платы и наличия теплоотвода от платы (металлической рамки).
Для платы из гетинакса с теплоотводом Кз =1.83*10-3.
Для платы из гетинакса без теплоотвода Кз =2.12*10-3.
Для платы из стеклотекстолита с теплоотводом Кз =1.57*10-3.
Для платы из стеклотекстолита без теплоотвода Кз =1.95*10-3.
3. Определяем перепад в зазоре между платой и направляющими:
Dtз = Pпл · Rз, где Рпл - мощность ячейки, Вт.
2 этап для тепловой схемы ТС 3
Расчет проводится на основании закона Фурье.
1. Определяем эффективную площадь поверхности параллелепипеда между микромодульным массивом и внутренней поверхностью корпуса, отстоящей от микромодульного массива на расстоянии, соответствующего золотому сечению 0.67 от массива:
Fэф = Fi + 0.54 dз min Sli + 1.2 dз min2, где Fэф - площадь поверхности микромодульного массива, м2;
Sli - сумма всех 12 ребер микромодульного массива, м;
dз min - минимальная величина зазора между корпусом и микромодульным массивом.
2. Определяем тепловое сопротивление зазора:
, где lз
- коэффициент теплопроводности воздуха,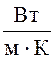 
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.