Занятие № 12. “Определение оптимальных маршрутов в сетях связи”
1. Алгоритмы маршрутизации с коммутацией каналов (на примере матричного алгоритма)
Наиболее распространенными алгоритмами маршрутизации в автоматизированных сетях телефонной связи являются различные модификации матричного алгоритма. Матричный метод относится к детерминированным методам динамического управления потоками и может быть как централизованным, так и децентрализованным.
Матричный алгоритм эффективен в случаях, когда при поиске оптимальных путей вводятся ограничения на максимальное число транзитных вершин в пути, что и определяет его практическое применение в сетях с коммутацией каналов.
Данный алгоритм получил свое название потому, что его можно описать, используя вместо тернарной операции операцию возведения матриц в степень. В матричном алгоритме при заданных i иj , когда k принимает все возможные значения, выполнение операции последовательного возведения в степень r приводит к определению веса оптимального пути между крайними вершинами графа при условии, что этот путь содержит не более одной, двух, . . . , (r –1) транзитной вершины.
Алгоритм осуществляет поиск оптимальных путей (по критерию минимальной длины) при ограничениях на максимальное число транзитных центров коммутации в пути. В его основе лежит матричный метод определения длин кратчайших путей между всеми узлами сети, основанный на применении операций над матрицами расстояний.
Структуру сети с указанием длин ветвей можно описать в
виде матрицы расстоянийL, в которой элемент ![]() – длина ветви между КЦi и КЦ j,
причем
– длина ветви между КЦi и КЦ j,
причем ![]() =
=![]() при
отсутствии ветви, а
при
отсутствии ветви, а ![]() =
0. Длина ветви
=
0. Длина ветви ![]() определяется
расстоянием между узлами сети или другим параметром (например, стоимостью),
пропорциональным длине. Матричный алгоритм позволяет сформировать ПРН,
оптимальный по критерию минимума длины ветвей в устанавливаемом соединении.
определяется
расстоянием между узлами сети или другим параметром (например, стоимостью),
пропорциональным длине. Матричный алгоритм позволяет сформировать ПРН,
оптимальный по критерию минимума длины ветвей в устанавливаемом соединении.
Рассмотрим алгоритм для сети, структура которой показана на рис. 1.
|
|
|
Рис. 1. Структура сети и матрица расстояний L
Если всем элементам матрицы L
присвоить значение единицы (![]() ),
то можно построить план, оптимальный по минимуму числа транзитных ЦК в пути.
),
то можно построить план, оптимальный по минимуму числа транзитных ЦК в пути.
Для определения длин кратчайших путей между всеми
узлами сети матрица расстояний L возводится в степень r ![]() N – 1 , где N – число
узлов сети. Вычисление более высокой степени прекращается, если в процессе
вычисления будет иметь равенство
N – 1 , где N – число
узлов сети. Вычисление более высокой степени прекращается, если в процессе
вычисления будет иметь равенство
![]() .
.
Это равенство означает, что кратчайшие пути между каждой парой узлов находятся среди одно, двух, . . . , (r – 1) – транзитных путей, а любой путь с числом транзитов, больше чем r, не является кратчайшим.
Матрица ![]() называется дистанционной.
Ее элементы равны длинам кратчайших путей между соответствующими узлами сети.
называется дистанционной.
Ее элементы равны длинам кратчайших путей между соответствующими узлами сети.
При возведении матрицы L в степень r используются следующие правила:
1. Операция умножения элементов матрицы ![]() и
и ![]() соответствует их алгебраической сумме:
соответствует их алгебраической сумме: ![]() .
.
2. Основные правила сложения элементов матрицы:
0 + 0 = 0; ![]() +
+ ![]() =
=
![]() ;
; ![]() +
0 =
+
0 = ![]() ;
; ![]() ;
;
![]() +
+ ![]() =
=
![]() .
.
3. Значение элемента новой матрицы принимается по критерию минимума длины ветвей.
Используя данные правила, возведем матрицу L
в квадрат (L![]() = L
= L![]() L
L![]() ),
при этом получим элементы
),
при этом получим элементы ![]() матрицы
L
матрицы
L![]() ,которые равны длине кратчайшего пути от ЦКi
к ЦКj среди всех путей с одним транзитным узлом:
,которые равны длине кратчайшего пути от ЦКi
к ЦКj среди всех путей с одним транзитным узлом:
![]() .
.
Это означает, что для получения 1-го элемента 1-й
строки матрицы L![]() складываются почленно элементы 1-й строки с
элементами 1-го столбца матрицы L.
складываются почленно элементы 1-й строки с
элементами 1-го столбца матрицы L.
Для получения 2-го элемента 1-й строки матрицы L![]() складываются почленно элементы 1-й строки с элементами
2-го столбца матрицы L.
складываются почленно элементы 1-й строки с элементами
2-го столбца матрицы L.
Для получения 3-го элемента 1-й строки матрицы L![]() складываются почленно элементы 1-й строки с
элементами 3-го столбца матрицы L и т.д.
складываются почленно элементы 1-й строки с
элементами 3-го столбца матрицы L и т.д.
Так, например, при возведении матрицы L, для сети показанной на рис. 1, в квадрат, получим элементы 1-й строки:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Аналогичным образом находятся элементы 2-й, 3-й и 4-й
строк. Матрица L![]() имеет вид:
имеет вид:
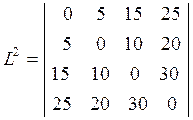 .
.
При возведении матрицы L в степень r
= 3 получим матрицу ![]() ,
элементы которой равны длине кратчайшего пути между
,
элементы которой равны длине кратчайшего пути между ![]() и
и ![]() среди
всех путей с одним и двумя транзитными ЦК:
среди
всех путей с одним и двумя транзитными ЦК: ![]() . Так, при возведении матрицы L,
показанной на рис. 1, в степень r =3, получим следующие элементы 1-й строки:
. Так, при возведении матрицы L,
показанной на рис. 1, в степень r =3, получим следующие элементы 1-й строки:
![]()
![]() и
т.д.
и
т.д.
В результате матрица L![]() имеет
вид:
имеет
вид:
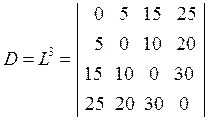 .
.
Элементами этой матрицы являются длины кратчайших
путей между любыми центрами коммутации, в состав которых входят одна, две или
три ветви (один или два транзитных ЦК). Матрица ![]() является дистанционной: D = L
является дистанционной: D = L![]() = L
= L![]() . Элементы дистанционной матрицы
. Элементы дистанционной матрицы ![]() определяются по матрице L
определяются по матрице L![]() .
Однако в дистанционной матрице D не заложено дополнительных
сведений о составе путей. Поэтому при матричном методе дополнительно
используются следующие операции:
.
Однако в дистанционной матрице D не заложено дополнительных
сведений о составе путей. Поэтому при матричном методе дополнительно
используются следующие операции:
1. Формирование матриц очередности выбора исходящих ветвей (статических детерминированных таблиц маршрутов) для каждого центра коммутации.
2. Проверка и исключение наличия петель в путях первого, второго, третьего выбора.
2. Алгоритмы маршрутизации в сетях с коммутацией пакетов (на примере алгоритма Дейкстры)
Исходными данными для реализации алгоритма являются
матрица весов ![]() ,
начальная вершина
,
начальная вершина ![]() ,
критерий оптимальности opt и операция над весами двух смежных ребер
,
критерий оптимальности opt и операция над весами двух смежных ребер ![]() . Конечной целью является нахождение веса оптимального
пути из начальной вершины
. Конечной целью является нахождение веса оптимального
пути из начальной вершины ![]() в
конечную вершину
в
конечную вершину ![]() графа.
графа.
Алгоритм включает в себя четыре шага, выполняемых последовательно.
Шаг 1.Формирование начальных условий.
Все множество вершин разбивается на два подмножества.
Первое из них содержит только начальную вершину ![]() ,
а второе (Т) – все остальные вершины:
,
а второе (Т) – все остальные вершины: ![]() .
.
Шаг 2.Определение очередной вершины, исключаемой из множества Т.
Определяется такая вершина ![]() , для которой выполняется равенство
, для которой выполняется равенство ![]()
![]() .
.
Если найдется несколько вершин, удовлетворяющих этому условию, то выбирается любая из них.
Шаг 3.Корректировка матрицы весов W и вектора путей DH.
Исключить из множества Т вершину ![]() и для всех вершин
и для всех вершин ![]() выполнить тернарную операцию вида
выполнить тернарную операцию вида ![]() .
.
Если ![]() изменит
свое значение, то есть если
изменит
свое значение, то есть если ![]() ,
то d (j) = i.
В противном случае соответствующий элемент вектора DH
не изменяется.
,
то d (j) = i.
В противном случае соответствующий элемент вектора DH
не изменяется.
Шаг 4.Определение конца процесса.
Если мощность множества Т равна единице, то все оптимальные пути найдены. В противном случае осуществляется переход к выполнению шага 2.
Рассмотрим пример определения оптимальных путей от
вершины ![]() ко
всем остальным вершинам графа (рис. 1).
ко
всем остальным вершинам графа (рис. 1).
Исходные данные:
· матрица расстояний L;
·
начальная вершина графа ![]() ;
;
· критерий оптимальности – {min}.
На шаге 1
осуществляется формирование начальных условий: вектор путей ![]() , множество вершин
, множество вершин ![]() , так как вершина 1 – начальная (
, так как вершина 1 – начальная (![]() ).
).
Первая итерация.
На шаге 2 первой итерации определяется вершина, исключаемая из множества Т.
При этом ![]() , то есть выбирается ребро
, то есть выбирается ребро ![]() . Следовательно,
. Следовательно, ![]() .
Вершина
.
Вершина ![]() ,
соответствующая пути оптимального веса, исключается из множества Т (
,
соответствующая пути оптимального веса, исключается из множества Т (![]() ) и присоединяется к множеству,
содержащему начальную вершину
) и присоединяется к множеству,
содержащему начальную вершину ![]() .
Множество
.
Множество ![]() .
.
На шаге 3 первой итерации для множества вершин 3,4 выполняются тернарные операции с целью корректировки матрицы весов W и вектора DH. При этом:
![]() , то есть вес
, то есть вес ![]() изменил
своё значение, при этом
изменил
своё значение, при этом ![]() имеет значение
имеет значение ![]() ;
;
![]() . В данном случае вес
. В данном случае вес ![]() так же изменил
своё значение, поэтому
так же изменил
своё значение, поэтому ![]() ;
;
Таким образом, первая строка матрицы весов W
приобретает вид ![]() , а вектор путей
, а вектор путей ![]() .
.
На шаге четвёртом первой итерации определяется мощность множества T, которая равна 2, следовательно, осуществляется переход к шагу 2 второй итерации.
Вторая итерация.
На шаге 2 второй итерации определяется очередная вершина, исключаемая из множества
Т. При этом ![]() . Следовательно,
. Следовательно, ![]() ,
исключается вершина 3 (
,
исключается вершина 3 (![]() ) и остается множество вершин
) и остается множество вершин ![]() .
.
На шаге 3 второй итерации корректируются W и DH. При этом:
![]() .
Таким образом,
.
Таким образом, ![]() ,
, ![]() .
.
Тогда первая строка матрицы весов W остается в
прежнем виде ![]() , так же как и вектор путей
, так же как и вектор путей
![]() .
.
Поскольку мощность множества T на шаге 4 второй итерации определяется как 1, поэтому процесс определения оптимальных путей завершается. Пути содержатся в модифицированном векторе D1, а их веса – в первой строке модифицированной матрицы W.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.