Распространение пучков с большим нормированным первеансом, страница 6

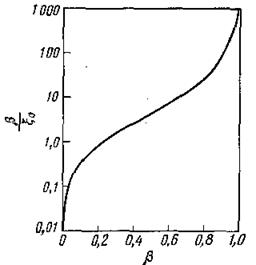
Как можно видеть, медленные ионы почти всегда составляют существенную часть плазмы пучка и во многих случаях их плотность гораздо выше плотности ионов пучка. Малые значения β делают до некоторой степени некорректным использование выражения (6.12), ниже мы вернемся к этому обстоятельству. Пока лишь отметим, что ошибка такова, что полученное выше значение β слишком велико для условия малости β.

Чтобы найти потенциал пучка относительно стенок, необходимо вычислить скорость генерации и потерь электронов. Обозначив вводимый на единицу высоты пучка электронный ток как I_el, получим

.                                                         (6.17)

Положим I_el=γI_blи сделаем те же подстановки, что и в (6.14), для того чтобы получить (6.15), тогда имеем

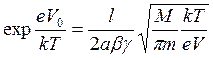.                                                         (6.18)

Комбинируя (6.18) с соотношением (6.16), получим выражение

,                                                         (6.19)

что приводит к

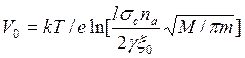.                                                         (6.20)

Для того чтобы оценить последнее соотношение, посмотрим на величины в выражении в скобках правой части (6.20). Зададим l=2 м и М/m=7,3∙10⁴ (для ионов аргона). Для малых значений σ_с и n_а выше мы получили β=0,75 при ξ₀=0,04. Для довольно больших γ, например γ=0,5, имеем

.                                                         (6.21)

Большие значения σ_с и n_а, использованные выше, привели к β≪1 при ξ₀=0,34. Взяв малое γ=0,1, получим выражение

.                                                         (6.22)

Можно считать, что значение логарифма большого числа столь нечувствительно к самому числу, что можно пренебречь изменением численного коэффициента и положить

V₀≃7kT/e.                                                         (6.23)

Кроме проанализированной здесь ситуации были рассмотрены случаи, когда быстрые ионы вызывают ионизацию в пучке и когда ионизация вызвана электронами, пронизывающими пучок. Вряд ли целесообразно проводить здесь рассмотрение всех случаев. Поскольку скорость потерь электронов изменяется как ехр(-eV₀/kT), все эти случаи приводят к логарифмической зависимости потенциала, лежащей в пределах между значениями, задаваемыми формулами (6.21) и (6.22), т. е. удовлетворительно аппроксимируемой зависимостью (6.23).

Нечувствительность логарифма к величине аргумента вызывает вопрос о том, существенно ли использование при анализе зависимости (6.12) или нет. Ошибка в три раза в величине аргумента приводит к изменению численного множителя в (6.23) всего на единицу, даже десятикратная ошибка прибавит всего 2,3. Таким образом, можно сказать, что потенциал довольно хорошо определен в единицах электронной температуры, даже вели поперечное к пучку движение ионов, описываемое (6.13), есть предмет специального рассмотрения.

Вычисления, проведенные выше в разд. 6.2, вряд ли являются идеальным расчетом профиля потенциала поперек пучка даже в идеализированном одномерном случае с постоянной плотностью пучка. Следует сшить решение в пучке с решением, удовлетворяющим условиям между пучком и стенкой. Имея эту информацию и зная электронную температуру, можно вычислить расходимость пучка. Насколько нам известно, такие детальные вычисления выполнены не были, но поставлен ряд интересных экспериментов, в которых величина V₀ измерялась и сопоставлялась с расширением пучка в разных условиях.

В. Экспериментальные результаты

В экспериментах Крау однородный и однонаправленный пучок ионов аргона Аr⁺ с энергией 500 эВ и большим нормированным первеансом формировался с помощью ускоряющей системы из двух мелкоячеистых сеток (см. рис. 5.32), описанной в разд. 5.10. Расплывание пучка определялось по току на зонды, которые двигались поперек пучка в двух сечениях, как показано на рис. 6.7. Большой плоский эмиттер электронов, подогреваемый безындукционным способом (на рис. 6.7 это не показано), мог генерировать широкий пучок электронов, которые могли быть ускорены при помощи тонкой вольфрамовой сетки. Поперек ионного пучка экспериментальное оборудование включало также электромагнит, изображенный условно на рис. 6.7, способный создавать поперечное однородное магнитное поле в объеме, занимаемом второй половиной пучка. Магнитное поле, напряженность которого изменялась до 0,025 Т, являлось слабым для ионов, поскольку их ларморовский радиус был велик по сравнению с протяженностью их траекторий в области поля, но сильным для термализованных электронов, ларморовский радиус которых был мал по сравнению с любыми размерами пучка.